Mechanism Analysis of Start and Unstart Flow Characteristic Structures of a Supersonic Inlet
-
摘要: 基于Wagner等实验的超声速进气道模型, 采用RANS-SST计算方法分析超声速进气道起动和不起动流场特性。通过拓宽计算域和采用来流边界层自由发展方法, 准确预测了典型的进气道不起动过程中可能出现的周期性振荡流现象, 包括进气道内部高压的产生和降低、下壁面大尺度分离泡的膨胀收缩和迁移, 并伴随不起动激波的传播。进气道完全起动状态(末端活门挡板角度β=0°)时得到的波系结构、壁面压强和流向速度分布计算结果与实验测量值相吻合; 不起动状态(β=28°)时流场的振荡周期和振幅与实验结果一致。对进气道不起动的非定常流场进行动态模态分解, 发现了3个特征频率: 主频f1=69.8 Hz的流场模态揭示了进气道出口的压强振荡最强, 而入口及上壁面的速度振荡最强; 二倍频f2=139.7 Hz和三倍频f3=209.5 Hz捕捉到的流场模态主要是离散的小尺度高能结构。在不起动状态的振荡过程中, 进气道入口外部流场产生了较大的速度和压力脉动, 所以对进气道内外流场相互作用的准确描述是预测不起动状态振荡流动的重要因素。Abstract: Based on the supersonic inlet model in Wagner's experiment, RANS-SST was used in numerical simulation to analyze the inlet start and unstart flow field characteristics. By broadening the computational domain and adopting the free development method of boundary layer, the possible periodic oscillatory flow phenomena in the process of the inlet unstart, such as the high-pressure generation and reduction inside the inlet, the expansion and contraction of large-scale separation bubbles at the lower wall, and the unstart shock propagation, were accurately predicted. For inlet start at the flap angle of 0, the wave structures, wall pressure, and flow velocity distributions were consistent with the existing experimental results. For inlet unstart at the flap angle of 28, the oscillation period and amplitude of the flow field were in agreement with the experimental data. The dynamic mode decomposition of the unsteady flow of the inlet unstart was carried out. In the flow field mode with the main frequency f1=69.8 Hz, the pressure oscillation at the outlet of the inlet is the strongest, while the velocity oscillation at the inlet and the upper wall is the strongest. In addition, the flow field modes captured by double frequency f2=139.7 Hz and triple frequency f3=209.5 Hz are mainly discrete small-scale high-energy structures. In the oscillation process of the inlet unstart, the flow field outside the inlet produces large velocity and pressure pulsation. Therefore, the accurate description of the interaction between the fields inside and outside the inlet is an important factor to predict the inlet unstart oscillatory flow.
-
Keywords:
- inlet /
- unstart /
- oscillatory flow /
- shock wave /
- dynamic mode decomposition
-
引言
超声速进气道作为冲压发动机的重要组成部分，能够在起动状态下工作是确保推进系统正常运行的基本要求[1-2]。
关于进气道不起动问题，自1944年Oswatisch[3]首次观察到超声速进气道入口振荡流动以来，国内外针对这种特殊的振荡现象进行了大量的研究[4]。Wagner等[5-7]对Mach数为5的超声速进气道进行了风洞实验，在隔离段末端安装挡板来模拟背压，通过改变挡板角度，观察到进气道起动、不起动现象，发现不起动状态下进气道内存在3种不同振幅和频率的振荡流动，并且振荡流动中存在激波的运动。Tan等[8]对来流Mach数为5的矩形进气道的不起动振荡流进行了实验研究，提出以对流、激波串运动和声波传播共同建立反馈回路这一新的振荡机制，使用该机制估计的振幅和频率与实验结果基本一致。Chang等[9]通过实验研究了来流Mach数为4.5~6.0时进气道的不起动流动，观察到两种新的振荡模式，即混合振荡模式和间歇振荡模式，为认识进气道振荡流机理、预测和控制进气道不起动提供了参考。中国科学技术大学的Li等[10]在不同出口节流比下对来流Mach数为5.9的高超声速进气道进行了实验研究，发现在低节流比下进气道起动，而在近堵塞节流比下进气道不起动，并且出现激波振荡现象，振荡频率随节流比的增加而增加。
得益于数值仿真技术的发展与应用，超声速进气道数值模拟方法可以对进气道不起动问题进行仿真预测，并提供详细的流场信息分析不起动机理。袁化成等[11]对二维高超声速进气道的不起动和再起动过程进行了数值分析，发现进气道不起动后能否再起动与来流Mach数有关；常军涛等[12]对高超声速进气道二维流场进行了数值模拟，从流动稳定性的角度解释了进气道不起动/再起动特性形成的原因。Koo等[13]利用大涡模拟(large eddy simulation, LES)方法对Wagner的实验进行了数值研究，准确预测了进气道起动状态下的流场特征；但对于进气道不起动状态，由于没有考虑风洞实验中实际的内外流耦合情况，Koo等[13]的LES结果没有得到实验中观察到的振荡模式。
LES面向流动精细化结构分析时具有较好的求解能力，但是计算代价较高，在使用其计算进气道内外流的耦合问题时对计算能力仍然存在较大的挑战。本文基于Wagner实验中的超声速进气道实验模型，采用Reynolds平均Navier-Stokes(Reynolds averaged Navier-Stokes, RANS)数值计算方法，拓宽计算区域表征内外流场耦合条件和来流湍流边界层发展情况，分析Ma=5进气道在起动和不起动状态下的定常和非定常流场，并通过动力学模态分解(dynamic mode decomposition, DMD)方法对进气道不起动振荡流进行模态特征分析。
1. 物理模型及数值仿真方法
1.1 物理模型
本文数值模拟分析所采用的研究对象是Wagner等[5-7]在德克萨斯大学风洞中开展实验的物理模型，如图 1所示。该模型由长度L1=90.7 mm的内收缩进气道和长度L2=242.3 mm的等截面隔离段组成，其中进气道入口收缩角α=6°，入口高度H0=34.9 mm，隔离段高度h=25.4 mm，模型内部宽度W=2h=50.8 mm。在隔离段出口设置了活门挡板装置，实验中通过调整挡板角度(β=0°~28°)改变通流面积，以此模拟发动机燃烧产生的反压，从而观察进气道从起动状态到不起动状态的流动变化过程。表 1给出了实验中提供的自由来流条件，来流Mach数为4.9，总温Tt为330 K、总压Pt为2.5 MPa。实验通过纹影成像技术对激波结构进行观察分析，同时采用粒子图像测速(particle image velocimetry, PIV)成像技术测量流场。在实验模型的下壁面设置了7个压强监测点T1~T7(见图 1(a))，记录壁面压强随时间的变化情况。实验中进气道入口前的来流边界层为湍流边界层，并测得来流条件下入口下壁面T1位置边界层厚度(99%U∞)为19.3 mm，静压为5 380 Pa。
Tt/K Pt/MPa Ma V/(m/s) 330 2.5 4.9 740 1.2 数值仿真方法
1.2.1 计算模型和边界条件
本文计算基于CFX软件，使用有限体积法求解三维可压缩完全气体Navier-Stokes方程[14]，空间离散采用迎风格式，并采用SST湍流模型[15-16]对进气道的起动和不起动状态分别进行RANS和URANS计算。收敛残差设置为1.0×10-6，亚迭代步数为10，URANS计算的时间步长为1.0×10-6 s。
图 2给出了本文根据实验物理模型得到的计算模型。超声速进气道模型的长度为13.11h，高度为1.38h。为了保证计算边界条件与风洞实验条件更好地保持一致，计算区域拓展到实验件前60h、后7h，纵向宽度扩展到20h。针对进气道不起动状态，除了β=0°工况外，还设置了β=20°, 21°, 22°, 23°, 25°, 28°的计算模型(见图 2(a))，分别计算特定β角度下进气道内部的流动。计算入口边界条件设为超声速进口给定来流条件，计算域下边界及进气道表面设为无滑移绝热壁面，上边界及下游出口边界为超声速出口边界条件。计算域展向宽度设为h，两侧设为周期性边界。
1.2.2 计算网格及方法校验
针对进气道模型(β=0°)设计了4套不同的网格方案，以验证数值方法的网格无关性，进气道局部网格如图 2(b)所示，表 2为具体的网格参数，其中网格1与网格2中第1层网格高度均为0.08 mm，而网格3与网格4中第1层网格高度为0.05 mm。图 3给出了4套网格计算得到的壁面压强分布与实验测量值[5]和他人LES结果[13]的比较，可以发现除了网格1计算得到的压强曲线有两处明显的凸起变化，网格3和网格4的压强分布基本保持一致，说明网格3的精度已经能够满足RANS计算需求，因此选择网格3开展进一步计算分析。相关计算结果与参考文献中的LES结果也较吻合，与实验结果基本保持一致。因此，本文基于网格3(y+=9)的设置参数完成不同β角度模型的网格划分，模型网格单元总量约为1.8×106个。
表 2 网格参数Table 2. Grid parameterscase total elements initial layer thickness/mm grid 1 5.94×105 0.08 grid 2 9.86×105 0.08 grid 3 1.469×106 0.05 grid 4 2.243×106 0.05 ![]()
图 3 不同网格的壁面压强分布曲线Figure 3. Wall pressure distribution curves under different grid resolutions2. 结果与讨论
2.1 完全起动状态
β=0°时，进气道完全起动，计算得到的数值仿真结果如下。进气道入口前T1壁面处的流向速度沿高度方向的变化曲线如图 4所示，进气道入口来流条件与实验中的来流条件吻合较好：T1处的湍流边界层厚度为17.78 mm(0.7h)，与实验测量值19.3 mm基本一致；计算得到T1点静压为5 314 Pa，实验测量值为5 380 Pa，相对误差为-1.2%。
如图 5(a)所示为实验[6]得到的起动状态下流场纹影图，可以看到其中存在复杂的波系结构。图 5(b)为计算得到的进气道对称面纹影图和压强云图，比较实验和计算结果可以发现，数值模拟成功捕捉到了实验中观测到的1, 2, 3这3道反射激波、膨胀波B以及上壁面边界层A。由于实验测量装置的限制，无法在实验中测量进口段的入射激波S，而计算结果可以得到更完整的激波结构, 从而分析进气道内的流动特征。
![]()
图 5 进气道对称面纹影图和压强分布Figure 5. Schlieren diagram and pressure contours at symmetry plane of the inlet他人研究指出激波边界层相互作用是影响进气道内部流动的主要因素之一[17-18]，图 6是图 5(b)纹影图的红框区域，为数值计算得到的局部流场结构，与激波与边界层作用的理论流场结构基本一致[19]，即入射激波与湍流边界层相互作用后引起湍流边界层气流分离，在分离区的分离点和再附点分别产生一道激波，并在下游相交。
![]()
图 6 激波和湍流边界层相互作用流场结构Figure 6. Flow field structure of interaction between shock waves and turbulent boundary layer图 7为隔离段x/h=4.5~10.5范围的流向速度分布云图，图 8为该范围内不同位置(x/h=4.5, 6.5, 8.5, 10.5)的流向速度分布曲线，RANS计算结果与实验测量值整体上基本一致，与参考文献中的LES结果也比较吻合，说明RANS对进气道内部流动的预测较好。
2.2 β对进气道不起动特性的影响
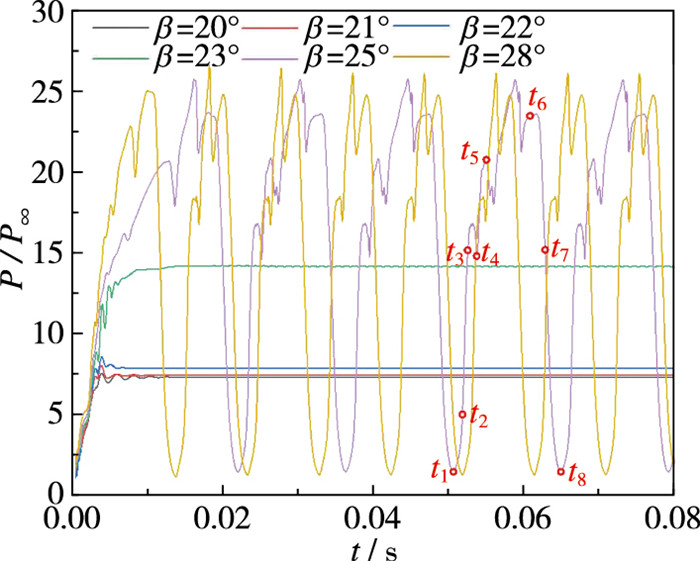
通过改变β大小，对进气道进行非定常仿真计算，得到β=20°, 21°, 22°, 23°, 25°, 28°共6个工况的计算结果。图 9是计算得到的各工况T7点压强随时间的变化曲线。对于β=20°, 21°, 22°，流场完全发展后T7点压强已不再随时间变化，分别稳定在7.34P∞, 7.47P∞, 7.88P∞。β=23°时，计算稳定后T7点压强在14.18P∞~14.25P∞范围内波动，振幅只有0.08P∞，考虑到计算误差，可以认为β=23°时流动是定常的。而β=25°和28°时，T7点压强随时间呈现周期性大幅振荡模式变化，周期分别为14.5 ms和9.5 ms，振幅分别为24.31P∞和25.35P∞，前者的振幅略小而周期较大；相应地，每个周期内β=25°的T7点压强比β=28°多一个极大值。
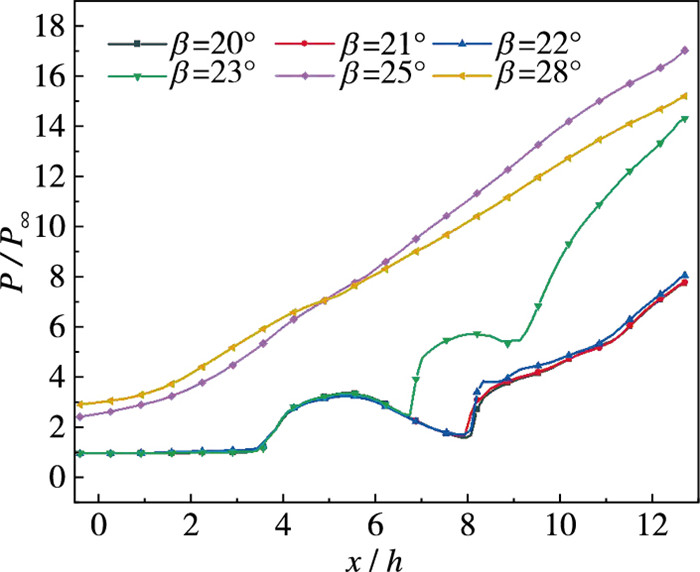
图 10为不同β对应工况下的进气道对称面的平均压强分布云图，与β=0°的流场相比，活门挡板抬起后，出口气流受阻导致气流压强升高，将造成出口堵塞引起进气道不起动。其中β=20°, 21°, 22°的进气道内部流场完全发展后保持稳定状态，由于三者β相差不大，对应的流场结构基本一致；并且由于中压区稳定在下游，并未向上游传播，此时流场中仍存在入射激波S、膨胀波B、反射激波1和2，进气道此时还可以起动。而β=23°时，出口附近压强较高，相比于β=20°~22°，高压区向上游发展，阻止了反射激波2的形成。注意到β=20°~23°的流场中，高压区前存在一道激波，将其称为不起动激波。β=25°和28°的平均流场中，高压气流几乎占满了整个通道，容易导致进气道出口气流反向流动，并且高压区阻断了入射激波的发展，没有形成反射激波，进气道为不起动状态。
![]()
图 10 进气道在不同β下的平均压强分布Figure 10. Average pressure contours of the inlet at different angles of β为了定量比较β对进气道内部流动的影响，图 11给出了不同β对应的进气道下壁面平均压强分布曲线。从图中可知，进气道壁面压强沿程逐渐增加；其中，β=20°~23°对应的压强突增点为激波所在位置。比较不同β对应的压强曲线，发现随着β的增大，壁面压强逐渐增大；并且β=23°时，进气道出口附近的压强相比于β=22°显著增加，结合前文分析，可以认为β=23°为进气道进入大幅周期性振荡不起动模式的临界角度。
![]()
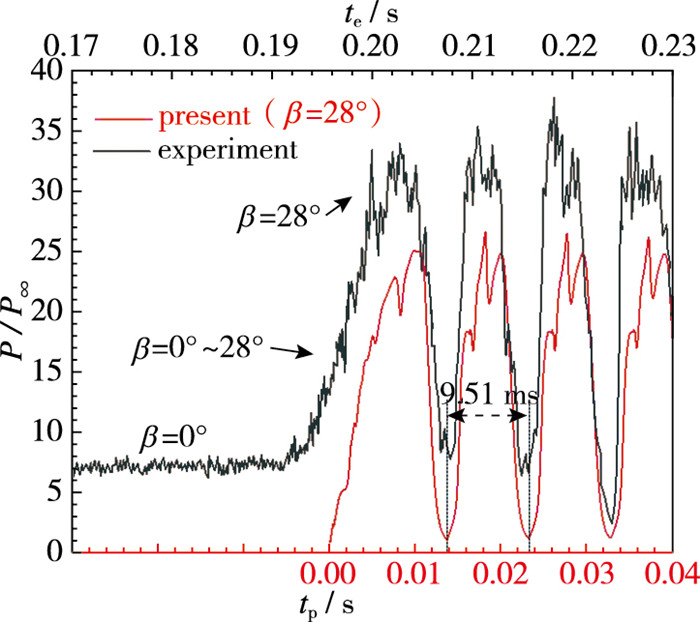
图 11 不同β下壁面平均压强分布曲线Figure 11. Average wall pressure distribution curves at different angles of β图 12是β=28°时数值计算和实验[6]的T7点压强变化曲线，其中黑色实线为参考文献中的实验结果，红色实线为计算结果。对比实验与计算结果，虽然数值计算和实验结果由于初始设置不同在压力脉动的峰谷值上存在一定差异，但T7点压强随时间变化的周期和振幅基本一致，周期为9.51 ms左右，振幅均在25P∞左右，因此数值计算具有一定的可信度。
![]()
2.3 不起动流场及其DMD特性分析
2.3.1 流场发展过程
β=25°时进气道内部流动表现为高度非定常性，图 9也表明此时流场结构呈周期性变化，是典型的进气道不起动流动模式。
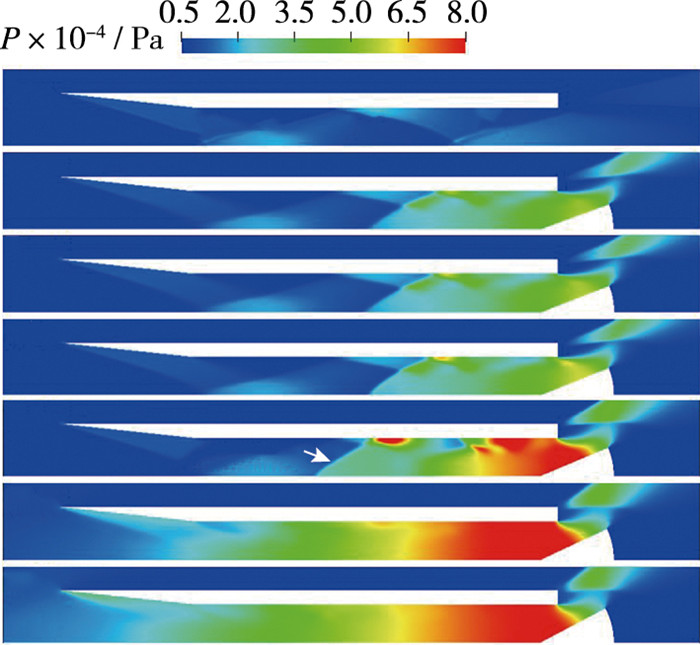
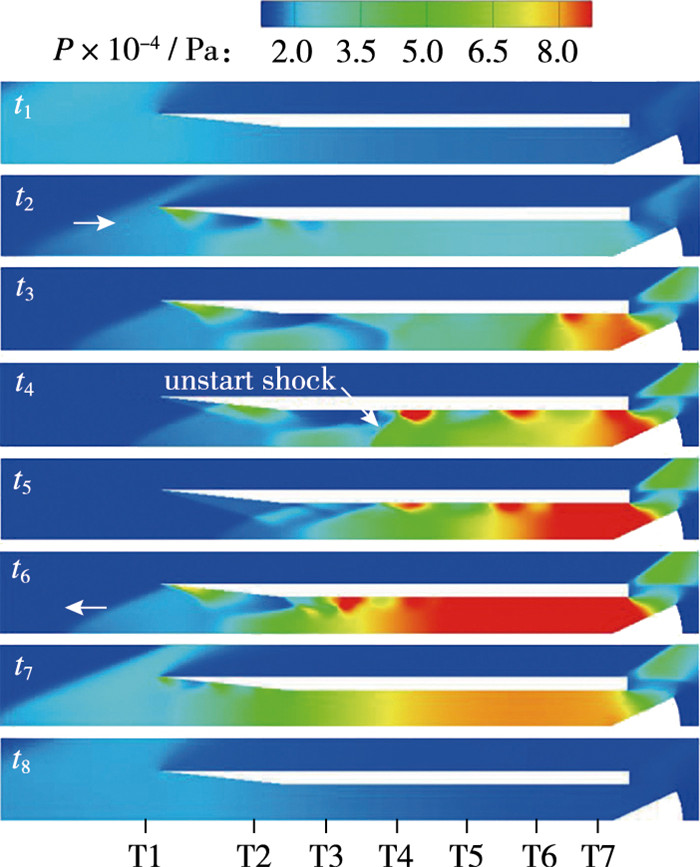
图 13，14分别为β=25°时一个周期内进气道流场发展过程的压力场和流线图，图中t1~t8时刻与图 9对应。在t1时刻，进气道入口被大尺度分离泡V1堵住，高速自由来流被阻挡在进气道外。但由于进气道内部压强较低，自由来流逐渐推动分离泡V1向下游移动并逐渐缩小，使得高速气流能够从上部分入口进入进气道(t2)，注意到分离泡V1前的弱激波也随之向进气道内部移动。当气流持续进入后，由于出口气流受挡板阻挡并且出口面积减小，在t3时刻，出口附近开始出现高压区，逆压梯度导致下壁面形成回流，出现分离区V2，由于高压逐渐扩大，在上游形成不起动激波(t4)，分离区V2向上游延伸至不起动激波后，而主流区主要分布在V1和V2之间，且沿上壁面向下游流动，这也抑制了上壁面分离泡的发展。
![]()
图 13 β=25°的进气道对称面压强分布随时间的变化Figure 13. Time history of pressure distribution on the symmetry plane of the inlet at β=25°![]()
图 14 β=25°的进气道对称面流线随时间的变化Figure 14. Time history of streamlines on the symmetry plane of the inlet at β=25°分离泡V1随自由来流继续向进气道内移动，并由于进气道入口主流面积的扩大，分离泡V1逐渐缩小，同时也因为大量气流到达下游，高压区进一步扩大，下游的分离区V2也推动不起动激波向前传播，直至V1融入V2，V1前的弱激波也将耗散(t5)，高速主流主要沿上壁面分布，此时入口起动，有更多气流进入进气道内。在t6时刻，进气道中下游充满高压气流，不起动激波后的分离区膨胀，为其提供前传的能量，此时不起动激波上缘恰好位于进气道入口；随着分离泡继续膨胀、不起动激波向进气道外传播，将入口堵住阻挡了高速自由来流，入口不起动，进气道内的高压气流将从出口排出，压强降低(t7)。当进气道下游压强降至来流水平，不起动激波前传至约x/h=-8后不再前传，此时(t9)流场结构与t1时一致，不起动激波将随来流向下游移动，进入下一周期。
上述结果表明，与β=20°~23°相比，β=25°时，进气道不起动流场中存在不起动激波的前传播、分离气泡的膨胀收缩和迁移以及下游高压区的产生与降低等流动特征，此时的进气道不起动是高度非定常流动的过程；并且由于计算域向前及纵向拓展，使得不起动激波和分离泡发展至进气道入口前，与自由来流相互作用，获得返回进气道内的能量，从而形成周期性振荡流动。
由于β=28°时进气道不起动的流动情况与β=25°类似，这里不再赘述。表 3分别列出了β=25°、28°时进气道不起动流中不起动激波从下壁面T5点传播到T1点的平均速度以及流场的振荡周期和主频率，其中频率为周期的倒数。对比可得β=25°时不起动激波的平均传播速度较小，相应的流动周期较长。
表 3 不起动激波的平均传播速度Table 3. Average propagation speed of unstart shockβ/(°) shock speed/(m/s) oscillatory period/ms oscillatory frequency/Hz 25 79.01 14.5 68.96 28 92.15 9.5 105.26 2.3.2 DMD特性分析
由Schmid[20]提出的动力学模态分析方法提供了一种从均匀采样非定常流场中提取动力学信息的工具，能够用于分析流场复杂的流动特征。与快速Fourier变换(fast Fourier-transform, FFT)相比，DMD的特点在于从复杂流场中提取单一频率的流动模态，并且可以通过各模态的特征描述流动随时间的演化过程，具有时空耦合的独特优势[20-22]。DMD能够帮助研究人员关注特定的流动特征和潜在的物理机制，同样可以用于进气道不起动振荡流的后处理分析。
对β=25°进气道对称面流场进行DMD处理，选取530个样本数据，采样频率为10 000 Hz。将530个时间点的流场数据导入Antares程序[23]进行分析，提取其动态变换过程的特征值和特征模态。其中得到的DMD频谱分布如图 15所示，幅值A随频率f的增加呈现下降趋势，即低频模态的幅值较大，其中幅值最大的模态频率为0 Hz，为静止模态。运动模态最大的频率是f1=69.8 Hz，这个频率与2.2节β=25°流场的振荡周期(14.5 ms)对应的主频相近。另外DMD频谱也包含了各个倍频，如二倍频f2=139.7 Hz、三倍频f3=209.5 Hz。
图 16, 17分别为DMD处理后，主频f1对应压力场和速度场的幅值和相位图。从压力场幅值分布中可以看到进气道出口附近的流场脉动最强，整体上脉动强度向上游递减，入口上壁面也存在中等脉动强度的流团。相位图表明隔离段内流场动态变化的相位差不大，但与入口上壁面流团的相位差约为π/2，与进气道入口及入口外的流动相位差约为π，说明进气道内部和入口压力的动态变化是反向的。从图 17速度场模态的幅值分布中可以发现峰值主要集中在上壁面中段(x/h=5~9)，入口段(x/h=0~5)上壁面附近以及入口前至下壁面x/h=-8处的幅值也较大，而从x/h=-2.5到下游，沿下壁面附近的幅值偏小，并且进气道出口附近整个通道内的幅值都较小，说明进气道内部中上游的上壁面以及入口前气流速度的变化程度较大，结合2.3.1节，发现这是由于入口大尺度分离泡和上壁面小尺度分离泡的运动造成的流场动态特征。另外，虽然图 17(b)相位图中进气道上下壁面附近的颜色差异较大，但由于相位差约为2π，说明两个区域的速度变化是连续的，而入口下壁面分离涡所在区域与其他流域的相位差约为π，即分离涡的运动与进气道内其他流动变化是相反的。
![]()
图 16 频率f1对应DMD模态的幅值和相位(压力场)Figure 16. Amplitude and phase of DMD mode at frequency f1(pressure field)![]()
图 17 频率f1对应DMD模态的幅值和相位(速度场)Figure 17. Amplitude and phase of DMD mode at frequency f1 for velocity相对于f1的高频运动模态也有助于理解流场动态变化的规律，图 18为f2，f3频率对应DMD模态的压力场分布。其中f2的流场特征结构沿上壁面分布；f3的流场结构除在上壁面外，还包括流道中部和挡板附近。与图 16相比，这两个频率下的流场模态主要是离散的小尺度高能结构。
![]()
图 18 f2，f3对应DMD模态的幅值(压力场)Figure 18. Amplitudes of DMD modes at frequencies f2 and f3(pressure field)3. 结论
本文基于Wagner等实验的超声速进气道实验模型，采用RANS-SST计算方法分析超声速进气道起动和不起动流场特性。通过计算域向前和纵向拓展，不仅得到与风洞实验基本一致的来流湍流边界层厚度和进气道入口条件，还能够满足进气道内外流场相互作用的条件，从而在计算分析中得到不起动振荡流动特征。
针对不同β模型的计算，发现随着β的增大，进气道出口和壁面压强逐渐增加，进气道由起动状态进入不起动状态。其中β=20°, 21°, 22°, 23°，流场为无振荡稳定模式；β=25°, 28°，流场为大幅低频振荡模式，进气道不起动。在β=0°的进气道完全起动流中，计算得到的壁面压强分布、不同站位流向速度分布均与实验测量值相吻合；β=28°不起动工况中的振荡周期和振幅与实验测量值一致。
对β=25°流场动态发展过程的分析发现进气道不起动是由出口面积减小造成压强增加导致的。相比于前人LES计算，拓展计算域后实现了进气道内外流的耦合，得到典型的进气道不起动振荡流，主要流动特征为出口高压区向上游的发展及压强再次降低、下壁面大尺度分离泡的膨胀收缩和前后移动，并伴随不起动激波的前后传播。对β=25°的流场进行DMD分析，得到流动主频f1=69.8 Hz、二倍频f2=139.7 Hz、三倍频f3=209.5 Hz。其中频率f1的流场模态表明进气道出口附近的压力场振荡最强、速度变化较弱，而出口附近和上壁面的速度场振荡较强。与f1相比，高频f2、f3捕捉到的流场模态主要是离散的小尺度高能结构。
-
![]()
图 3 不同网格的壁面压强分布曲线
Figure 3. Wall pressure distribution curves under different grid resolutions
![]()
图 5 进气道对称面纹影图和压强分布
Figure 5. Schlieren diagram and pressure contours at symmetry plane of the inlet
![]()
图 6 激波和湍流边界层相互作用流场结构
Figure 6. Flow field structure of interaction between shock waves and turbulent boundary layer
![]()
图 10 进气道在不同β下的平均压强分布
Figure 10. Average pressure contours of the inlet at different angles of β
![]()
图 11 不同β下壁面平均压强分布曲线
Figure 11. Average wall pressure distribution curves at different angles of β
![]()
![]()
图 13 β=25°的进气道对称面压强分布随时间的变化
Figure 13. Time history of pressure distribution on the symmetry plane of the inlet at β=25°
![]()
图 14 β=25°的进气道对称面流线随时间的变化
Figure 14. Time history of streamlines on the symmetry plane of the inlet at β=25°
![]()
图 16 频率f1对应DMD模态的幅值和相位(压力场)
Figure 16. Amplitude and phase of DMD mode at frequency f1(pressure field)
![]()
图 17 频率f1对应DMD模态的幅值和相位(速度场)
Figure 17. Amplitude and phase of DMD mode at frequency f1 for velocity
![]()
图 18 f2，f3对应DMD模态的幅值(压力场)
Figure 18. Amplitudes of DMD modes at frequencies f2 and f3(pressure field)
Tt/K Pt/MPa Ma V/(m/s) 330 2.5 4.9 740 
下载: 导出CSV
表 2 网格参数
Table 2 Grid parameters
case total elements initial layer thickness/mm grid 1 5.94×105 0.08 grid 2 9.86×105 0.08 grid 3 1.469×106 0.05 grid 4 2.243×106 0.05
下载: 导出CSV
表 3 不起动激波的平均传播速度
Table 3 Average propagation speed of unstart shock
β/(°) shock speed/(m/s) oscillatory period/ms oscillatory frequency/Hz 25 79.01 14.5 68.96 28 92.15 9.5 105.26
下载: 导出CSV
-
[1] Voland R, Auslender A, Smart M, et al. CIAM/NASA Mach 6.5 scramjet flight and ground test[R]. AIAA-99-4848, 1999.
[2] Walker S, Rodgers F, Paull A, et al. HyCAUSE flight test program[R]. AIAA 2008-2580, 2008.
[3] Oswatisch K. Der Druckrückgewinn bei Geschossen mit Rückstossantrieb bei Hohen Übershallgeschwindigkeiten[R]. Rept. No. 1005, 1944.
[4] Chang J T, Li N, Xu K J, et al. Recent research progress on unstart mechanism, detection and control of hypersonic inlet[J]. Progress in Aerospace Sciences, 2017, 89: 1-22. DOI: 10.1016/j.paerosci.2016.12.001
[5] Wagner J, Valdivia A, Yuceil K, et al. An experimental investigation of supersonic inlet unstart[R]. AIAA 2007-4352, 2007.
[6] Wagner J, Yuceil K, Valdivia A, et al. PIV measurements of the unstart process in a supersonic inlet/isolator[R]. AIAA 2008-3849, 2008.
[7] Wagner J L, Yuceil K B, Valdivia A, et al. Experimental investigation of unstart in an inlet/isolator model in Mach 5 flow[J]. AIAA Journal, 2009, 47(6): 1528-1542. DOI: 10.2514/1.40966
[8] Tan H J, Sun S, Yin Z L. Oscillatory flows of rectangular hypersonic inlet unstart caused by downstream mass-flow choking[J]. Journal of Propulsion and Power, 2009, 25(1): 138-147. DOI: 10.2514/1.37914
[9] Chang J T, Wang L, Bao W, et al. Novel oscillatory patterns of hypersonic inlet buzz[J]. Journal of Propulsion and Power, 2012, 28(6): 1214-1221. DOI: 10.2514/1.B34553
[10] Li Z F, Gao W Z, Jiang H L, et al. Unsteady behaviors of a hypersonic inlet caused by throttling in shock tunnel[J]. AIAA Journal, 2013, 51(10): 2485-2492. DOI: 10.2514/1.J052384
[11] 袁化成, 梁德旺. 高超声速进气道再起动特性分析[J]. 推进技术, 2006, 27(5): 390-393, 398. DOI: 10.3321/j.issn:1001-4055.2006.05.002 Yuan H C, Liang D W. Analysis of characteristics of restart performance for a hypersonic inlet[J]. Journal of Propulsion Technology, 2006, 27(5): 390-393, 398(in Chinese). DOI: 10.3321/j.issn:1001-4055.2006.05.002
[12] 常军涛, 于达仁, 鲍文. 攻角引起的高超声速进气道不起动/再起动特性分析[J]. 航空动力学报, 2008, 23(5): 816-821. DOI: 10.13224/j.cnki.jasp.2008.05.008 Chang J T, Yu D R, Bao W. Characteristic analysis of unstart/restart of hypersonic inlets caused by variations of attack angle of freestream[J]. Journal of Aerospace Power, 2008, 23(5): 816-821(in Chinese). DOI: 10.13224/j.cnki.jasp.2008.05.008
[13] Koo H, Raman V. Large-eddy simulation of a supersonic inlet-isolator[J]. AIAA Journal, 2012, 50(7): 1596-1613. DOI: 10.2514/1.J051568
[14] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006. Yan C. Computational fluid dynamics methods and applications[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2006(in Chinese).
[15] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI: 10.2514/3.12149
[16] Forsythe J R, Hoffmann K A, Suzen Y B. Investigation of modified Menter's two-equation turbulence models for supersonic applications[R]. AIAA 1999-0873, 1999.
[17] Dolling D S. Fifty years of shock-wave/boundary-layer interaction research: what next?[J]. AIAA Journal, 2001, 39(8): 1517-1531. DOI: 10.2514/2.1476
[18] 张悦, 谭慧俊, 王子运, 等. 进气道内激波/边界层干扰及控制研究进展[J]. 推进技术, 2020, 41(2): 241-259. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS202002001.htm Zhang Y, Tan H J, Wang Z Y, et al. Progress of shock wave/boundary layer interaction and its control in inlet[J]. Journal of Propulsion Technology, 2020, 41(2): 241-259(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS202002001.htm
[19] Anderson Jr J D. Modern compressible flow: with historical perspective[M]. 3rd ed. Boston: McGraw-Hill, 2003.
[20] Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5-28. DOI: 10.1017/S0022112010001217
[21] 寇家庆, 张伟伟. 动力学模态分解及其在流体力学中的应用[J]. 空气动力学学报, 2018, 36(2): 163-179. https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201802001.htm Kou J Q, Zhang W W. Dynamic mode decomposition and its applications in fluid dynamics[J]. Acta Aerodynamica Sinica, 2018, 36(2): 163-179(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201802001.htm
[22] 王建明, 王涵, 桂琳. 压气机叶栅叶顶间隙流的动力学模态分解[J]. 推进技术, 2018, 39(3): 520-527. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201803005.htm Wang J M, Wang H, Gui L. Dynamic mode decomposition of tip clearance flow in a compressor cascade[J]. Journal of Propulsion Technology, 2018, 39(3): 520-527(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS201803005.htm
[23] Team A D. Antares Documentation Release 1.20.0[CP/OL]. https://cerfacs.fr/antares/.
计量
- 文章访问数: 154
- HTML全文浏览量: 33
- PDF下载量: 24
邮件订阅
RSS