Processing math: 0%
主管部门： 中国航天科技集团有限公司
主办单位： 中国航天空气动力技术研究院
中国宇航学会
中国宇航出版有限责任公司

基于真实气体效应的湍流标度律特性

陈小平, 窦华书

陈小平, 窦华书. 基于真实气体效应的湍流标度律特性[J]. 气体物理, 2017, 2(4): 1-6. DOI: 10.19527/j.cnki.2096-1642.2017.04.001
引用本文: 陈小平, 窦华书. 基于真实气体效应的湍流标度律特性[J]. 气体物理, 2017, 2(4): 1-6. DOI: 10.19527/j.cnki.2096-1642.2017.04.001
shu
CHEN Xiao-ping, DOU Hua-shu. Characteristics of Turbulent Scaling Law in Real Gas Effects[J]. PHYSICS OF GASES, 2017, 2(4): 1-6. DOI: 10.19527/j.cnki.2096-1642.2017.04.001
Citation: CHEN Xiao-ping, DOU Hua-shu. Characteristics of Turbulent Scaling Law in Real Gas Effects[J]. PHYSICS OF GASES, 2017, 2(4): 1-6. DOI: 10.19527/j.cnki.2096-1642.2017.04.001
shu

基于真实气体效应的湍流标度律特性

  • 浙江省流体传输技术研究重点实验室，浙江理工大学，浙江杭州 310018

基金项目: 

国家自然科学基金 11502236

浙江省自然科学基金 LQ16E090005

浙江理工大学科研启动基金 ZSTU11130032611303

详细信息
    作者简介:

    陈小平(1985-)男, 江西赣州, 讲师, 研究方向为空气动力学, 计算流体力学.通信地址:浙江理工大学机械与自动控制学院(310018).E-mail:chenxp075@163.com

  • 中图分类号: O354

Characteristics of Turbulent Scaling Law in Real Gas Effects

  • Key Laboratory of Fluid Transmission Technology of Zhejiang Province, Zhejiang Sci-Tech University, Hangzhou 310018, China

摘要

    摘要
  • 摘要: 在量热完全气体、热完全气体和化学反应完全气体等3种气体模型假设下，利用Mach数为4.05、壁温为1 300 K的超声速槽道湍流的直接数值模拟（direct numerical simulation，DNS）结果，对标度律和自相似性做了详细分析.结果表明，不仅在量热完全气体模型下存在标度律和扩展自相似性，而且在热完全气体和化学反应完全气体模型下标度律和扩展自相似性仍然成立.压缩性的影响使得速度结构函数通过Favre平均获得更为合适.与热完全气体模型的结果相比，化学反应完全气体和量热完全气体模型的结果吻合更好.
    Abstract: In order to analyze the scaling law and extended self-similarity in detail, temporally evolving supersonic turbulent channel flows (reference Mach number at 4.05 and wall temperature at 1 300 K based on the wall parameters) were simulated using direct numerical simulation (DNS) approach. The gas models include calorically perfect gas, thermally perfect gas and chemically reacting gas in non-equilibrium ('chemically reacting gas' for short). The two later kinds of models are called by a joint name as the real gas models. It is found that the scaling law and extended self-similarity not only exist in calorically perfect gas, but also in real gas models. The Favre parameters are suitable to obtain velocity structure function because of the compressibility influence. The deviations between chemically reacting gas and calorically perfect gas provide better agreement than that between thermally perfect gas and calorically perfect gas.
    • HTML全文

  • 引言

    标度律是湍流研究的重要方法之一, 指的是湍流场惯性区内两点间速度差的统计矩(速度结构函数)与这两点间的距离成幂次变化关系.标度律最早由Kolmogorov提出, 并在此基础上给出了K41理论.该理论认为湍流的标度律是普适的, 且标度指数与统计阶次p之间呈线性关系[1].

    近期实验和数值结果表明, 标度指数与统计阶数之间并不完全呈线性关系.为解释这种现象, 发现并提出了扩展自相似性(extended self-similarity, ESS)[2-3].根据ESS理论, 各阶速度结构函数之间呈幂次关系, 即

    〈|δui|p〉~〈|δui|q〉ζp, q

    ζp, q为扩展的标度指数.目前, ESS理论已经在各向同性湍流[4]、槽道[5]及平板边界层[6-9]直接数值模拟(direct numerical simulation, DNS)中得到验证.对于考虑高温真实气体效应的超声速槽道湍流, 尚未见相关的标度律研究.

    当分子碰撞假定仅考虑弹性碰撞时, 低温流动经常被称为量热完全气体.然而, 在高速流动中, 边界层内的温度可能很高, 这将改变气体属性, 如比热及比热比变成温度的函数(热完全气体).当温度进一步升高, 化学反应(离解, 甚至电离)将会出现, 气体流动特征时间相当于化学反应特征时间, 气体将会处于一种化学反应, 这通常被称为化学反应完全气体.热完全气体和化学反应完全气体可统称为真实气体[10].然而在考虑真实气体效应时, 湍流标度律和自相似性是否仍然适用, 尚未研究清楚.

    在考虑真实气体效应(热完全气体和化学反应完全气体模型[11-13])情况下, 本文应用DNS进行了超声速槽道湍流的标度律研究.此外, 还给出了量热完全气体模型假设下的DNS结果.首先, 在量热完全气体模型假设下, 对比分析了超声速和亚声速槽道湍流下的标度律和自相关性, 然后重点分析了真实气体效应下的标度律.

    1.   控制方程及计算方法

    1.1   控制方程

    气体假定为热完全气体的混合物, 其化学反应速率为有限化学反应, 但不考虑振动激发的弛豫时间.此时, 控制方程为三维无量纲可压缩Navier-Stokes方程:

    \begin{array}{c} \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}(\rho {\mathit{\boldsymbol{u}}_j}) = 0\\ \frac{{\partial {\rho _s}}}{{\partial t}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left( {{\rho _s}{\mathit{\boldsymbol{u}}_j} - \frac{1}{{R{e_{{\rm{ref}}}}}}\rho {D_s}\frac{{\partial {Y_s}}}{{\partial {\mathit{\boldsymbol{x}}_j}}}} \right) = {w_s}\\ \frac{{\partial (\rho {\mathit{\boldsymbol{u}}_i})}}{{\partial t}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left( {\rho {\mathit{\boldsymbol{u}}_i}\cdot{\mathit{\boldsymbol{u}}_j} + p{\mathit{\boldsymbol{\delta }}_{ij}} - \frac{1}{{R{e_{{\rm{ref}}}}}}{\mathit{\boldsymbol{\sigma }}_{ij}}} \right) = \rho {\mathit{\boldsymbol{f}}_i}\\ \frac{{\partial E}}{{\partial t}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}[\left( {E + p} \right){\rm{ }}{\mathit{\boldsymbol{u}}_j} - \frac{1}{{R{e_{{\rm{ref}}}}}}({\mathit{\boldsymbol{u}}_i}\cdot{\mathit{\boldsymbol{\sigma }}_{ij}} + {\mathit{\boldsymbol{q}}_j} - \\ \sum\limits_s {} {\rho _s}{D_s}\frac{{\partial {Y_s}}}{{\partial {\mathit{\boldsymbol{x}}_j}}}{h_s})] = \rho {\mathit{\boldsymbol{f}}_i}\cdot{\mathit{\boldsymbol{u}}_i}\\ s = 1,{\rm{ }}2,{\rm{ }} \ldots ,{\rm{ }}ns - 1;{\rm{ }}i,{\rm{ }}j = 1,{\rm{ }}2,{\rm{ }}3 \end{array}

    其中, 组分由下标s表示, 矢量由下标i, j或k表示, δij为Kronecker符号, ws为组分s的非平衡源项, ρs为组分密度, ρ为混合气体密度, Ys=ρs/ρ为组分质量分数, uj为j方向的速度; p为压力; T为温度; hs为组分焓, Ds为扩散系数.总能E, 剪切应力张量σij和热通量qj定义为

    \begin{array}{c} E = \rho e + \frac{1}{2}\rho {\mathit{\boldsymbol{u}}_i}^2\\ {\mathit{\boldsymbol{\sigma }}_{ij}} = 2\mu {\mathit{\boldsymbol{S}}_{ij}} - \frac{2}{3}\mu {\mathit{\boldsymbol{\delta }}_{ij}}{S_{kk}},{\rm{ }}{\mathit{\boldsymbol{S}}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_j}}} + \frac{{\partial {\mathit{\boldsymbol{u}}_j}}}{{\partial {\mathit{\boldsymbol{x}}_i}}}} \right)\\ {\mathit{\boldsymbol{q}}_j} = k\frac{{\partial T}}{{\partial {\mathit{\boldsymbol{x}}_j}}} \end{array}

    其中, e为内能, Sij为应变率张量, μ为混合气体黏性系数, k为热传导系数.

    1.1.1   量热完全气体

    量热完全气体模型, 由于组分不发生变化, 因而仅须考虑总质量方程.此时, 内能仅是温度的函数, 比热比为常数且等于1.4, 黏性系数可通过Sutherland公式获得.

    1.1.2   热完全气体

    与量热完全气体模型相比, 热完全气体模型的主要特征是内能不仅有平动能和转动能, 而且包括被激发的振动能.因此, 比热及比热比不再是常数, 而是随着温度升高而改变[12].

    1.1.3   化学反应完全气体

    在仅考虑离解反应时, 本文所述的化学反应完全气体模型是指在反应热平衡、化学非平衡假设下得到.气体由O, O2, NO, N和N2这5种组分构成, 基元反应分别为

    \begin{matrix} {{\text{O}}_{\text{2}}}\text{+}M\rightleftharpoons \text{ 2O+}M \\ \text{NO+}M\rightleftharpoons \text{ N+O+}M \\ {{\text{N}}_{\text{2}}}\text{+}M\rightleftharpoons \text{ 2N+}M \\ {{\text{N}}_{\text{2}}}\text{+O}\rightleftharpoons \text{ NO+N} \\ \text{NO+O}\rightleftharpoons \text{ }{{\text{O}}_{\text{2}}}\text{+N} \\ \end{matrix}

    其他参量的具体描述可参看文献[11].

    1.2   计算方法

    表 1给出了高速高温槽道湍流的壁面参数, 即本文的无量纲参数.计算沿流向和展向采用周期边界条件, 法向采用无滑移边界条件.固壁处的温度相等且恒定.计算在流向和展向采用等距网格, 法向采用非等距网格, 网格在壁面附近密集.基于黏性尺度的网格间距见表 2.

    表  1  壁面参数和初始条件
    Table  1.  Wall parameters and initial condition for DNS data
    parametersvalues
    density ρw*/(kg/m3)8.891×10-2
    temperature Tw*/K1 300
    speed of sound cw*/(m/s)722.73
    Reynolds number Rew8 620
    total temperature T0 */K4 550
    Mach number Mref4.05
    下载: 导出CSV 
    | 显示表格
    表  2  网格分辨率和计算区域
    Table  2.  Grid resolution and domain size for DNS data
    casesLxLyLzΔx+Δy+Δz+nxnynz
    MR4π24π/321.50.497.17201261201
    MT4π24π/324.40.478.10201261201
    MP4π24π/328.50.519.50201261201
    下载: 导出CSV 
    | 显示表格

    对于充分发展的槽道湍流, 流向和展向是均匀同性的, 因此可以在流向和展向采用周期边界条件.法向采用无滑移边界条件.为了保证流动不被衰减, 计算采用均匀体积力进行驱动.

    方程无黏部分在Steger-Warming矢通量分裂后采用7阶WENO格式离散.黏性部分采用8阶中心差分格式.时间方向推进采用显式的3阶Runge-Kutta方法.

    2.   湍流结果

    2.1   量热完全气体标度律分析

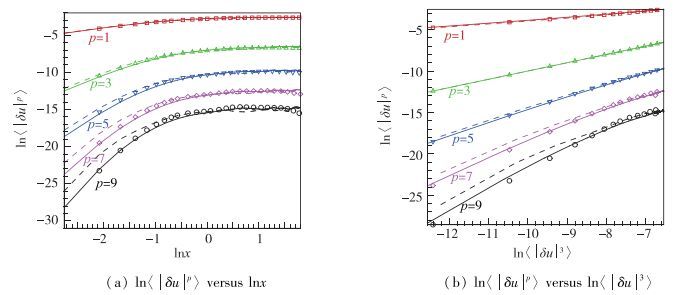
    在量热完全气体模型假设下, 图 1和图 2分别为y=0和y+=150处的标度律和扩散自相似性.为验证超声速槽道湍流的特征, 图中还给出了李新亮等[5]在Mach数等于0.8时的结果, 用实心点表示.从图中可以看出, 当p=1时, 本文模拟得到的结果与他人计算结果吻合; 但当p=3时, 本文的结果明显大于他人计算的结果, 并且随着p的增大, 两者的偏差越来越大.这可能是模拟工况存在一定区别导致的. 图 1(a)和图 2(a)为ln〈|δu|p〉与lnx的关系图.结果发现在对数坐标下, 所有的p速度结构函数与流向或展向方向在一定范围内都存在线性关系.这说明在超声速槽道湍流中, 中心线较宽区域内标度律成立.

    图  1  y=0处流向速度结构函数(红色线为Reynolds平均结果, 蓝色线为Favre平均结果, 点为Li等[5]结果)
    Figure  1.  Streamwise velocity structure functions at y=0(Red lines denote Reynolds average results, blue lines denote Favre average results, symbols denote Li et al[5]results)
    下载: 全尺寸图片 幻灯片
    图  2  y+=150处流向速度结构函数(红色线为Reynolds平均结果, 蓝色线为Favre平均结果, 点为Li等[5]结果)
    Figure  2.  Streamwise velocity structure functions at y+=150(Red lines denote Reynolds average results, blue lines denote Favre average results, symbols denote Li et al[5]results)
    下载: 全尺寸图片 幻灯片

    超声速湍流平均统计不仅有Reynolds平均, 还有Favre平均, 用{f}=〈ρf〉/〈ρ〉表示, 对应的脉动量可用f″表征.比较y=0和y+=150处的速度结构函数发现, Favre平均的结果整体小于Reynolds平均的结果, 而在y=0处两者的偏差减小.同时, 前者的结果整体更接近于李新亮等[5]的结果.这是由于Favre平均考虑了流场内部热力学量的影响, 更能表征超声速槽道湍流的标度律特征, 因此本文后续讨论都是基于Favre平均来开展的.

    图 1(b)和图 2(b)给出了上述流向速度结构函数的值, 横坐标改为ln〈|δu|3〉.从图中可以看出, 对于所有的p, ln〈|δu|p〉都与ln〈|δu|3〉存在良好的线性关系, 即超声速槽道湍流中心线附近较宽区域的自相似性也依然成立.

    2.2   真实气体效应的标度律分析

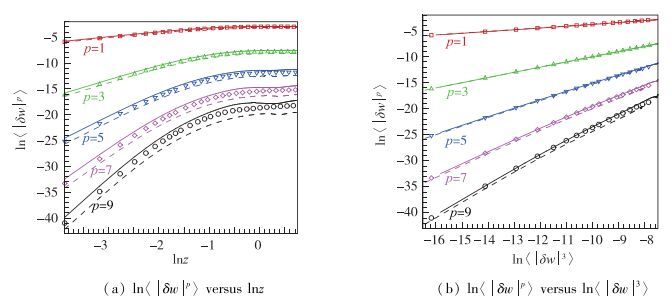
    在槽道中心(y=0) 处, 图 3给出了3种气体模型下流向速度结构函数, 其中图 3(a)的横坐标为lnx, 图 3(b)的横坐标为ln〈|δu|3〉.结果显示热完全气体和化学反应完全气体模型仅会部分影响超声速槽道湍流中的标度律和自相关性, 而不会破坏其规律.影响主要体现在热完全气体模型上, 当p阶数高时, 会在一定程度上偏离另外两种气体模型的结果, 并能够适当扩宽标度律和扩展自相似性的成立范围.

    图  3  y=0处3种气体模型流向速度结构函数(实线为量热完全气体结果, 虚线为热完全气体结果, 点为化学反应完全气体结果)
    Figure  3.  Streamwise velocity structure functions of three gas models at y=0(Solid lines denote calorically perfect gas results, dashed lines denote thermally perfect gas results, symbols denote chemically reacting gas results)
    下载: 全尺寸图片 幻灯片

    在槽道中心(y=0) 处, 图 4给出了3种气体模型下展向速度结构函数.从图中可以看出, 展向速度结构函数分布要比流向速度结构函数分布更好.同时, 3种气体模型得到的结果更为吻合.

    图  4  y=0处3种气体模型展向速度结构函数(实线为量热完全气体结果, 虚线为热完全气体结果, 点为化学反应完全气体结果)
    Figure  4.  Spanwise velocity structure functions of three gas models at y=0(Solids lines denote calorically perfect gas results, dashed lines denote thermally perfect gas results, symbols denote chemically reacting gas results)
    下载: 全尺寸图片 幻灯片

    2.3   相对标度律指数

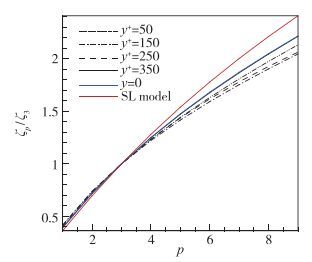
    图 5给出了本文得到的流向和展向标度指数和理论预测值.其一为由Kolmogorov提出的著名K41理论, 其标度率的计算公式为ζp/ζ3=p/3, 图中用K41表示; 其二为由She等[2]提出的标度律ζp/ζ3=p/9+2[1-(2/3) p/3], 该标度律是迄今被证明最普适的规律, 图中用SL model表示.结果表明, 流向和展向相对标度指数都与SL model标度律吻合较好, 当阶数增大时数值偏差增大, 与K41的结果相差较大. 图 5(a)还给出了李新亮等[5]计算的M=0.8的可压缩槽道湍流的标度指数, 发现其符合SL model标度律的范围大于本文的, 这可能是压缩性效应增强引起的变化.相似的结论在梁贤等[9]的平板边界层中提到.此外, 对比图 5(a)和(b), 可以看到展向相对标度指数偏离SL model标度律的幅值也明显小于流向的相对标度指数.

    图  5  3种气体模型下的相对标度指数(实线为y=0, 虚线为y+=150)
    Figure  5.  Relative scaling exponents of three gas models (Solid lines denote y=0, dashed lines denote y+=150)
    下载: 全尺寸图片 幻灯片

    在化学反应完全气体模型假设下, 图 6给出了不同法向位置处的流向相对标度律指数.结果显示近壁区标度律偏小, 当阶数增大时偏差增大, 这主要是近壁流动的强异性引起的.随着远离壁面, 相对标度律指数越来越接近SL model模型.

    图  6  不同法向位置的流向相对标度指数(化学反应完全气体)
    Figure  6.  Streamwise directional relative scaling exponents of chemically reacting gas
    下载: 全尺寸图片 幻灯片

    3.   结论

    在量热完全气体、热完全气体和化学反应完全气体假设下, 本文基于Mach数等于4.05, 且Rey-nolds数等于8 620的超声速槽道湍流的直接数值模拟数据, 重点分析了标度律和扩展自相似性, 得到如下结论:

    (1) 在量热完全气体假设下, 超声速槽道湍流的中心线附近较宽区域存在标度律和扩展自相似性.但由于压缩性的影响, 其速度结构函数通过Favre平均得到更为合适.

    (2) 热完全气体和化学反应完全气体模型获得的标度律和扩展自相似性仍然成立.

    (3) 与热完全气体模型的结果相比, 化学反应完全气体和量热完全气体得到的结果吻合更好.

  • 图  1   y=0处流向速度结构函数(红色线为Reynolds平均结果, 蓝色线为Favre平均结果, 点为Li等[5]结果)

    Figure  1.   Streamwise velocity structure functions at y=0(Red lines denote Reynolds average results, blue lines denote Favre average results, symbols denote Li et al[5]results)

    下载: 全尺寸图片 幻灯片

    图  2   y+=150处流向速度结构函数(红色线为Reynolds平均结果, 蓝色线为Favre平均结果, 点为Li等[5]结果)

    Figure  2.   Streamwise velocity structure functions at y+=150(Red lines denote Reynolds average results, blue lines denote Favre average results, symbols denote Li et al[5]results)

    下载: 全尺寸图片 幻灯片

    图  3   y=0处3种气体模型流向速度结构函数(实线为量热完全气体结果, 虚线为热完全气体结果, 点为化学反应完全气体结果)

    Figure  3.   Streamwise velocity structure functions of three gas models at y=0(Solid lines denote calorically perfect gas results, dashed lines denote thermally perfect gas results, symbols denote chemically reacting gas results)

    下载: 全尺寸图片 幻灯片

    图  4   y=0处3种气体模型展向速度结构函数(实线为量热完全气体结果, 虚线为热完全气体结果, 点为化学反应完全气体结果)

    Figure  4.   Spanwise velocity structure functions of three gas models at y=0(Solids lines denote calorically perfect gas results, dashed lines denote thermally perfect gas results, symbols denote chemically reacting gas results)

    下载: 全尺寸图片 幻灯片

    图  5   3种气体模型下的相对标度指数(实线为y=0, 虚线为y+=150)

    Figure  5.   Relative scaling exponents of three gas models (Solid lines denote y=0, dashed lines denote y+=150)

    下载: 全尺寸图片 幻灯片

    图  6   不同法向位置的流向相对标度指数(化学反应完全气体)

    Figure  6.   Streamwise directional relative scaling exponents of chemically reacting gas

    下载: 全尺寸图片 幻灯片

    表  1   壁面参数和初始条件

    Table  1   Wall parameters and initial condition for DNS data

    parametersvalues
    density ρw*/(kg/m3)8.891×10-2
    temperature Tw*/K1 300
    speed of sound cw*/(m/s)722.73
    Reynolds number Rew8 620
    total temperature T0 */K4 550
    Mach number Mref4.05
    下载: 导出CSV

    表  2   网格分辨率和计算区域

    Table  2   Grid resolution and domain size for DNS data

    casesLxLyLzΔx+Δy+Δz+nxnynz
    MR4π24π/321.50.497.17201261201
    MT4π24π/324.40.478.10201261201
    MP4π24π/328.50.519.50201261201
    下载: 导出CSV
    • 参考文献(13)
  • [1]

    Kolmogorov A N. Local structure of turbulence in an incompressible viscous fluid at very high Reynolds numbers[J]. Dokl Akad Nauk SSSR, 1941, 31:538-540.
    [2]

    She Z S, Leveque E. Universal scaling laws in fully developed turbulence[J]. Physical Review Letters, 1994, 72(3):336-339. DOI: 10.1103/PhysRevLett.72.336
    [3]

    Benzi R, Ciliberto S, Baudet C, et al. Extended self-similarity in the dissipation range of fully developed turbulence[J]. Europhysics Letters, 1993, 24(4):275-279. DOI: 10.1209/0295-5075/24/4/007
    [4]

    Rubesin M W. Extra compressibility terms for Favre-ave-raged two-equation models of inhomogeneous turbulent flows[R]. NASA CR-177556, 1990.
    [5] 李新亮, 马延文, 傅德薰.可压槽道湍流的直接数值模拟及标度律分析[J].中国科学(A), 2001, 31(2):153-164. http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK200102007.htm

    Li X L, Ma Y W, Fu D X. Direct numerical simulation of compressible channel flow and its scaling law analysis[J]. Science China Series A, 2001, 31(2):153-164(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JAXK200102007.htm
    [6]

    Amati G, Benzi R, Succi S. Extended self-similarity in boundary layer turbulence[J]. Physical Review E, 1997, 55(6):6985-6988. DOI: 10.1103/PhysRevE.55.6985
    [7]

    Li X L, Fu D X, Ma Y W. Direct numerical simulation of a spatially evolving supersonic turbulent boundary layer at Ma=6[J]. Chinese Physics Letters, 2006, 23(6):1519-1522. DOI: 10.1088/0256-307X/23/6/045
    [8]

    Liang X, Li X L. DNS of a spatially evolving hypersonic turbulent boundary layer at Mach 8[J]. Science China:Physics, Mechanics & Astronomy, 2013, 56(7):1408-1418. http://www.irgrid.ac.cn/handle/1471x/648506?mode=full&submit_simple=Show+full+item+record
    [9] 梁贤, 李新亮, 傅德薰, 等. Mach 8的平板可压缩湍流边界层直接数值模拟及分析[J].中国科学:物理学力学天文学, 2012, 42(3):282-293. http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201203010.htm

    Liang X, Li X L, Fu D X, et al. DNS and analysis of a spatially evolving hypersonic turbulent boundary layer over a flat plate at Mach 8[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2012, 42(3):282-293(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201203010.htm
    [10]

    Anderson J D. Hypersonic and high temperature gas dynamics[M]. New York:AIAA, 2000.
    [11]

    Chen X P, Li X L. Direct numerical simulation of chemical non-equilibrium turbulent flow[J]. Chinese Physics Letters, 2013, 30(6):064702. DOI: 10.1088/0256-307X/30/6/064702
    [12] 陈小平, 李新亮, 樊菁.变比热真实气体效应的高超声速槽道湍流直接数值模拟[J].中国科学:物理学力学天文学, 2011, 41(8):969-979. http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201108010.htm

    Chen X P, Li X L, Fan J. Direct numerical simulation of hypersonic turbulent channel flow in thermally perfect gas[J]. Scientia Sinica:Physica, Mechanica & Astronomica, 2011, 41(8):969-979(in Chinese). http://www.cnki.com.cn/Article/CJFDTOTAL-JGXK201108010.htm
    [13]

    Chen X P, Dou H S. Application of direct numerical si-mulation method to high Reynolds number turbulentchannel flow[C]. 2015 International Conference on Mechanical and Aeronautical Engineering(ICMAE 2015), Singapore, 2015.
    • 相关文章
    • 施引文献(1)

  • 期刊类型引用(0)

    其他类型引用(1)

    • 资源附件(0)
图(6)  /  表(2)
计量
  • 文章访问数:  56
  • HTML全文浏览量:  16
  • PDF下载量:  4
  • 被引次数: 1
出版历程
  • 收稿日期:  2016-12-02
  • 修回日期:  2016-12-17
  • 发布日期:  2017-07-19
  • 刊出日期:  2017-06-30

目录

摘要
HTML全文

  • 引言

  • 1.   控制方程及计算方法

  • 1.1   控制方程

  • 1.1.1   量热完全气体
  • 1.1.2   热完全气体
  • 1.1.3   化学反应完全气体

  • 1.2   计算方法

  • 2.   湍流结果

  • 2.1   量热完全气体标度律分析

  • 2.2   真实气体效应的标度律分析

  • 2.3   相对标度律指数

  • 3.   结论

参考文献(13)
相关文章
施引文献(1)
资源附件(0)

/

返回文章
返回

联系我们

联系电话：010-68192419

电子邮箱：qtwl@spacechina.com

官网网址：http://qtwl.xml-journal.net/

通信地址：北京市丰台区云岗西路17号，7201信箱34分箱《气体物理》编辑部（100074）

网站版权 © 京ICP备 12043220号-2

友情链接

邮件订阅
RSS

本系统由 北京仁和汇智信息技术有限公司 开发