Review of Spontaneous Capillary Driven Flow along Interior Corners
-
摘要: 文章从静力和动力学的角度简要回顾了关于沿内角的自发毛细流动研究的最近进展.作为一个通用几何形状,内角在地面微观尺度下或处于失重状态的航天飞行器系统内大尺度下为液体提供有效的输运通道.当一定的几何条件得到满足并且当毛细力远远大于体力比如重力的时候,沿着内角会发生自发毛细力驱动流动现象.从静力学的角度来说,本文讨论的自发毛细驱动流动和当特定的边界条件发生突然变化,比如重力作用突然消失时带有内角的容器内部单值有限高度的平衡自由面的非存在性有关系. Concus-Finn方法可以用来确定这样的平衡自由面在一个横截面处处一致的柱形容器内的非存在性.用这个方法可以推导出在失重状态下一个内角为2α的通常柱形容器里,当接触角小于π/2-α时,平衡曲面不存在.通常来说，沿内角的自发毛细驱动流动属于层流.利用尺度分析和摄动法，成功分析了该流动的动力学特性，并且推导出对设计有用的封闭形式的解析解.一个典型的结果是在黏性流的范畴里毛细面端点的移动和t1/2成正比Abstract: This paper briefly reviews the recent development in understanding the spontaneous capillary driven flow along interior corners from both static and dynamic point of views. Interior corners are a common geometric element for effective liquid transport in micro-scale in terrestrial condition or in large length scale in micro-gravity onboard spacecraft system. Spontaneous capillary driven flows take place along the interior corners when certain geometric conditions are satisfied and when capillary forces dominate body forces such as gravitational forces. From the static point of view, the spontaneous capillary driven flow discussed herein is related to the non-existence of equilibrium capillary surfaces in containers possessing the interior corners when certain boundary conditions undergo sudden changes such as gravity vanishing abruptly. The non-existence of the equilibrium surface in a cylindrical container of uniform cross section can be identified using Concus-Finn method. In a generic cylindrical container with an interior corner of 2α, the method can be applied to show that the equilibrium surface fails to exist in zero gravity when contact angle is less than π/2-α. In general the spontaneous capillary flow along the interior corners is in the regime of laminar flows. The dynamics of such flow has been analyzed successfully using scaling and perturbation method yielding closed form analytic solutions which are useful for design purpose. A typical result is that in the viscous regime the movement of the meniscus tip is proportional to t1/2.
-
引言
作为流体力学的一个分支, 毛细流体力学研究的是流体系统里具有气体和液体或不相溶的液体和液体之间的交界面, 交界面的形状或者整个流体系统的动力学特性主要是由表面张力或毛细力控制.简言之, 毛细流体力学研究的是由毛细力主控的毛细现象.交界面通常称作自由面, 当毛细力主控时, 交界面又称作毛细面.毛细面的形状可以自由改变, 以使表面自由能达到最小值.毛细力起主控作用意味着相比之下其他力(如惯性体力)是高阶小量, 即惯性体力/毛细力≪1.惯性体力和毛细力之比给出一个重要的无量纲参数——Bond数.当惯性体力是重力时, Bond数可以表达为
Bond=ΔρgL2σ (1) 其中，Δ ρ为交界面两边的流体的密度差, g为重力加速度, L为特征长度, σ为表面张力.重力和毛细力相比是高阶小量，即Bond«1意味着毛细现象在地球常规条件下可以在微观尺度(L~1 mm)上发生, 在失重或者微重力状态下则可以在宏观尺度(L~1 m)上发生.
对毛细现象的研究是一门经典的学科. Laplace和Thomas Young在这方面的工作为该学科的开创奠定了基础[1-3].和毛细现象相关的其他无量纲参数还包括Capillary数Weber数Marangoni数等, 限于篇幅, 本文集中探讨与小Bond数相关的一些毛细现象.
微观尺度下的毛细流动(例如多孔介质内的毛细流动)和石油开采技术联系紧密.宏观尺度下的毛细现象则和航天技术联系紧密.在近地轨道或者深度空间运行的飞行器上的液体推进剂管理和载人飞行系统里的废水收集与处理是两个和毛细流动现象相关的典型例子.本文侧重讨论与液体推进剂管理装置功能相关的毛细流动现象.
在轨道运行的飞行器需要经常启动反作用控制系统(reaction control system, RCS)的小型液体火箭发动机, 以保证飞行器的姿态及轨道.这些发动机所用的推进剂储存在液体燃料箱内.液体推进剂管理指的是在燃料箱被液体推进剂部分充满的条件下, 如何保证燃料箱出口处无气体掺杂的液体推进剂随时供给.例如, 有的早期燃料箱内部运用一个有弹性的皮囊(bladder)作为推进剂的容器, 当推进剂体积减少时, 皮囊会因为弹性自动收缩, 从而能有效保证燃料箱出口处的燃料供应.这个技术的缺点是皮囊的重量太大, 从而增加了整个飞行器系统的发射和运作费用.现代的燃料箱设计摒弃了皮囊这类技术, 而采用了充分利用毛细力的体积小重量轻的推进剂管理装置(propellant management devices).如果不用皮囊和其他任何手段, 在微重力状态下的外界干扰, 包括反作用控制系统发动机的点火所产生的作用在整个飞行器上的惯性力, 会使燃料箱内的液体推进剂移动到远离燃料箱出口的位置.当干扰消失时, 推进剂未必会自动流回到燃料箱的出口处.推进剂管理装置利用几何形状及毛细力使液体燃料自发地流回到燃料箱的出口处.
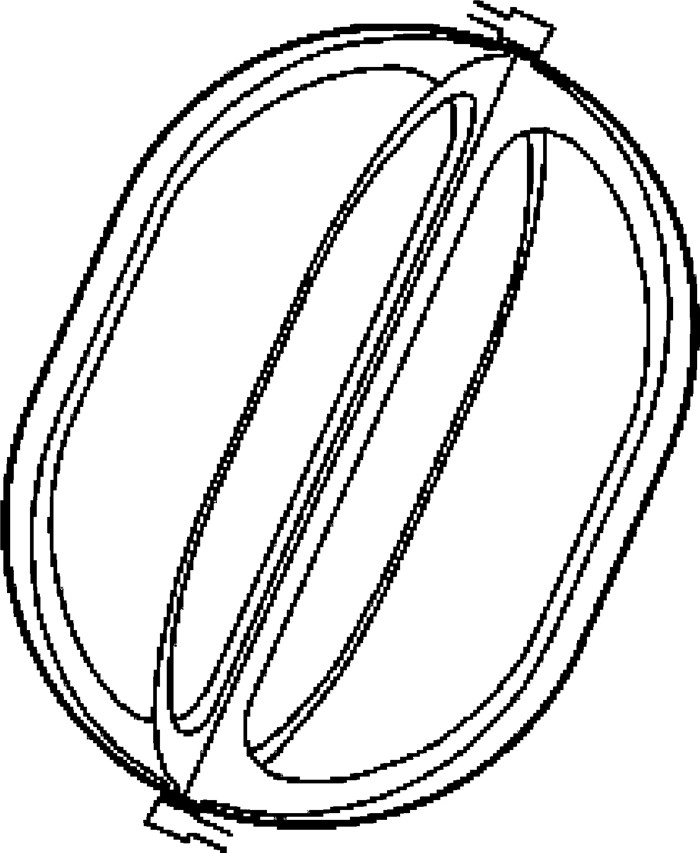
推进剂管理装置包括叶片(vane)[4]，海绵(sponge)[5]，笼(trap)[6]和闭合通道(gallery)[7]等.其中, 叶片是最简单有效的一种装置，如图 1所示.叶片安装在燃料箱的壁面附近及中央部位.当叶片接触壁面时，叶片的两面和燃料箱壁面形成两个独立的角落, 这样的角落通常被称为内角(interior corner), 见图 2.当叶片和壁面有一定缝隙时这两个角落通过缝隙连接起来.在中央部位叶片之间形成多个独立的内角.这些角落为自发毛细流动提供了有效的通道.本文先从静力学的角度探讨为什么内角能为毛细流动提供通道, 然后从动力学的角度描述沿着内角的毛细流动的特性.
![]()
图 1 液体燃料箱内的叶片式推进剂管理装置示意Figure 1. Schematic view of vane type propellant management device inside a fuel tank![]()
图 2 液体燃料箱叶片式推进剂管理装置横截面Figure 2. Cross-sectional view of vane type propellant management device1. 平衡毛细面及其存在性
忽略重力的情况下, 设想有一定体积的液体在一个未充满的高度无限的柱形容器里处于平衡状态, 见图 3.假设液体的体积足够覆盖容器的底部, 那么气体和液体之间的平衡交界面的形状s=u(x, y)由Young-Laplace-Gauss方程
\nabla \cdot \mathit{\boldsymbol{Tu = }}2\mathcal{H}, \mathit{\boldsymbol{Tu = }}\frac{{\nabla u}}{{\sqrt {1 + {{\left| {\nabla u} \right|}^2}} }} (2) ![]()
图 3 横截面均一的柱形容器内的毛细面示意(没有显示毛细面下方的液体)Figure 3. Schematic view of capillary surface within a cylindrical container of uniform cross section(liquid below capillary surface is not shown)和边界条件υ·Tu=cosγ描述; γ为通常说的接触角; \mathscr{H}为交界面上任何一点上的平均曲率, υ为容器侧面的法向单位矢量.
方程(2) 是一个非线性偏微分方程, 它的解在几何上是平均曲率处处相等的曲面.曲面上任意一点的平均曲率决定了交界面在该点两边的流体的压强差, 这个压强差由Young方程
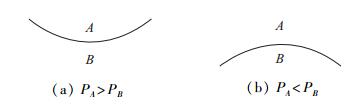
\Delta p = 2\sigma \mathcal{H} (3) 描述.对于一个处于流体A和B之间的交界面, 当交界面向流体B弯曲时, 流体A内部的压强大于流体B内部的压强, 如图 4(a); 反之, 流体A内部的压强小于流体B内部的压强, 如图 4(b).
![]()
图 4 流体压强和交界面弯曲方向的关系Figure 4. Sketches showing the relation between pressure difference and direction in which a surface curves在一些特殊的条件下, 方程(2) 有解析解.比如说, 当容器是圆柱形时, 那么方程的解是球面的一部分.当柱形容器的横截面不是圆形时, 球面只有在一些特定的条件下才是方程(2) 的解, 比如说规则的多边形.在高度无限的柱形容器里, 满足方程(2) 的平衡曲面和柱形容器的底部(也代表容器的横截面)上的每一点有着一一对应的关系, 或者说容器底部的每一点都被液体覆盖.这样的曲面具有平均曲率处处相等单值有限高度的性质. Concus等[8-10]发现在有些情况下方程(2) 无解.无解指的是上述的平衡曲面不存在.
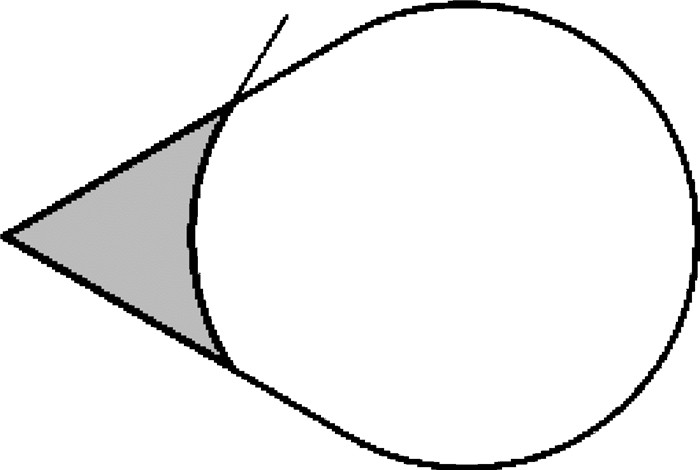
作为一个典型的例子, 取一个两边和圆弧相切的锐角, 把锐角和圆弧之间组成的封闭区域作为柱形容器的横截面, 如图 5所示, 把这个容器叫做单角柱形容器, 同时把这个锐角称为容器的内角.假设在重力作用下, 该容器的底部被一定量的液体覆盖, 由于重力作用, 液体和气体的交界面大部分和容器底部平行, 只有在靠近容器侧壁的地方气液交界面会呈现一定的曲度，以满足液体和容器侧壁面的接触角边界条件.可以只关心接触角γ在0~90°之间时的情形, 因为可以推导出当γ在90~180°之间时交界面的形态和当γ在0~90°之间时交界面的形态正好是相反的.
![]()
图 5 二维单角柱形容器的横截面形状Figure 5. Cross section of a two-dimensional cylindrical container with a single corner由于重力产生的静压作用, 交界面上的平均曲率不是处处相等，而是在每个方向上有一定梯度以平衡静压.当重力突然消失时, 液体会沿着平均曲率梯度产生的液体压力减小的方向流动,直到气液交界面重新达到平衡状态.当γ=90°时, 可以很容易得到交界面在新的平衡状态下是一个平面.当γ从90°开始减小时, 前面提到在无重力情况下圆柱形容器里的气液交界面的形状是球面的一部分,问题是在内角顶点的领域里交界面的形状应该是什么样的.如果在处于内角顶点的柱形容器的母线被液体覆盖部分上的某一点取一个容器的横截面，以至于该横截面上内角的邻域是液体，而其他部分则是气体, 如图 6所示.液体和气体部分之间的交界线则是气液交界面和该横截面的交线.交界线和内角的两边相交.如果忽略交界面在该交界线处沿着容器轴线方向的曲率，那么交界线和内角两边的交角和接触角相等.交界线的凹凸性由接触角γ以及内角的半角α决定.如果γπ/2-α, 那么交界线向液体部分弯曲或者说是凹型的, 见图 6; 如果γ>π/2-α, 那么交界线向气体部分弯曲或者说是凸型的; 如果γ=π/2-α, 那么交界线是一条直线.
![]()
图 6 二维单角柱形容器的横截面和液面的交界线Figure 6. Intersection line between cross section of a two-dimensional cylindrical container with a single corner and a liquid surface为了便于描述, 把液体自由面和位于内角顶点处柱形容器的母线的交点称为自由面的端点(meniscus tip).考虑在端点附近位于容器横截面上的交界线.当γ < π/2-α时, 交界线呈凹性, 并且离端点越近的交界线的曲率越大, 这就意味着和该交界线在同一平面内的液体内的压强越小, 结果是在自由面上沿着指向端点的方向存在着一个压力梯度, 这个压力梯度会一直驱动着内角附近的液体流向端点，从而使端点往远离容器底部的方向移动.注意液体的主体仍然位于容器靠近圆柱壁面的区域.主体的自由面更接近于一个球面, 这部分自由面的平均曲率比内角附近的自由面的平均曲率总是要小, 相应地主体液体内部的压强比内角附近液体的压强总是要大.在一个高度无限的单角柱形容器里, 无论有多少液体, 液体自由面也无法达到平衡状态.换言之, 在内角顶点的一个邻域里, 自由面离容器底部的距离最终会趋向无穷, 在这个意义上，方程(2) 无解或者说没有常规解[9].这种情形在γ≥π/2-α时不会发生, 方程(2) 总是有解.
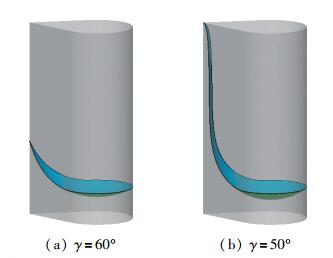
在实际应用中，任何一个容器的高度总是有限的. 图 7给出在有限高度开口单角柱形容器里的曲面的数值解, 其中内角的角度为60°. 图 7(a)中γ=π/2-α, 平衡曲面存在; 图 7(b)中γ < π/2-α, 方程(2) 无解, 表现为:液体会沿着内角分布一直达到容器开口处边缘而达到平衡状态, 由于容器高度有限, 自由面端点最终在容器的上方开口边缘被强制性地定住, 曲面是处于平衡状态, 但是平均曲率不是处处相等, 所以不是方程(2) 的解.
![]()
图 7 计算得到的单角柱形容器里的液体和气体之间的Figure 7. Numerical results of capillary surface shape in container with single corner (the liquid below the capillary surface is not shown)当γ < π/2-α时, 方程(2) 在单角柱形容器里无解的性质可以推广到任何一个带内角的柱形容器, 这是为什么叶片式推进剂管理装置里的内角能为液体燃料提供有效通道的机理.在液体燃料充分多的情况下, 如果燃料由于惯性力扰动而移动到和燃料箱(通常有圆柱段)出口相反部位, 当扰动消失时, 液体燃料会受毛细力的驱动沿着内角流回到燃料箱的出口.
对于一个具有一般横截面形状的无限高柱形容器, Concus和Finn[11]从理论上提供了一个方法, 用以判别液体自由面在该容器里是否具有平均曲率处处相等单值有限高度的平衡曲面.他们的方法称为Concus-Finn方法.
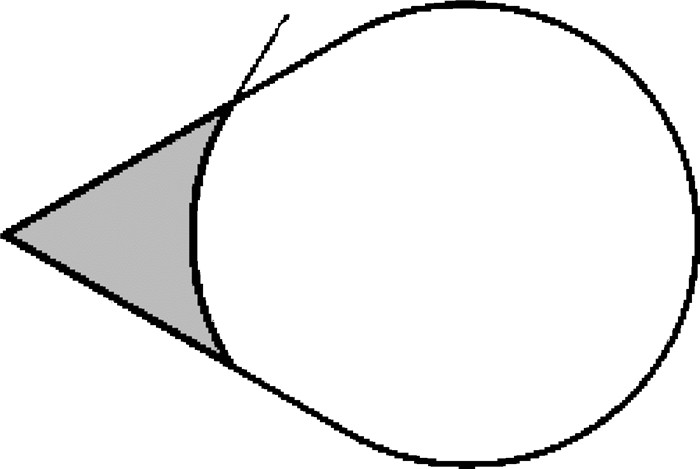
以单角柱形容器的横截面为例描述Concus-Finn方法.如图 8所示, Ω指容器的横截面并代表其总面积, Σ指横截面的边界并代表其总长度, γ代表液体和壁面之间的接触角.假设液体自由面和容器横截面相交的曲线是一个圆弧Γ, 其半径由
![]()
图 8 二维单角柱形容器横截面Figure 8. Cross section domain of a two-dimensional cylindrical container with single corner{R_\gamma } = \frac{\varOmega }{{\varSigma \cos \gamma }} (4) 给出. Γ与横截面边界的交角和γ相等.图中阴影部分代表Γ和横截面的一部分边界Σ*包围的一个横截面的子域，其面积由Ω*表示. Concus和Finn推导出一个定义在这个子域上的泛函数
\varPhi (\varGamma ) = \varGamma - (\cos \gamma ){\varSigma ^*} + \frac{{{\varOmega ^*}}}{{{R_\gamma }}} (5) 其中，Γ代表圆弧的弧长.具体地说, 对于每一个Γ, 如果Φ > 0, 那么单值有限高度的液体平衡自由面存在; 如果有任何一个Γ使得Φ ≤ 0, 那么单值有限高度的液体平衡自由面不存在, 自由面会在一个相应的子域Ωo上趋于无穷，并且Ωo \supseteq Ω*, 当Φ=0时, Ωo=Ω*.和Φ=0相对应的变量的值称为临界值, 比如说在Φ=0时的接触角的值是临界接触角值.在Φ=0时, 如果Γ>0那么平衡自由面不存在, 如果Γ=0那么平衡自由面仍然存在.
通常一个一般的横截面上容许上面描述的圆弧Γ的可能性的情况是有限多的, 这样可以通过对每个可能性评估Φ的值来确定在给定的容器里单值有限高度的液体平衡自由面是否存在.对于一个角度为2α的内角, 这个方法给出一个简洁的临界接触角表达式
{\gamma _c} = \frac{\pi }{2} - \alpha (6) Finn等[12]指出, 当满足方程(2) 的解的平衡自由面不存在时, 在一个无限高柱形容器里至少有一个奇异解存在.这样的奇异解被称为C-奇异解.在一个以规则多边形为横截面的柱形容器里的C-奇异解最先由de Lazzer等发现[13], Finn等后来给出了一个一般性的数学证明.以单角柱形为例, C-奇异解的思想核心是:在每一个使Φ≤0的Γ的附近会有至少一个圆弧Γo，其半径Ro≥Rγ, 在Γo和内角顶点之间的横截面的子域里, 自由面的高度趋于无穷, Γo的另外一边自由面渐进趋于与圆弧Γo重合的一个圆柱面, 图 7 (b)所示的曲面在一定程度上代表了这个趋势.
C-奇异解虽然属于静力学范畴, 但是Ro在下文将要阐述的对沿内角的一种毛细流动的分析里是一个重要的边界条件. Concus-Finn方法针对的是无限高度柱形容器, 但是这个方法对于弱三维容器仍然有效, 从而为流动提供动态边界条件[32].
内角和叶片式推进剂管理装置紧密相关. Concus和Finn对内角的钝度[14]以及内角两个面上的接触角的差异[15]的影响做了分析.另外一个需要考虑的参数就是叶片和壁面之间的缝隙.由于缝隙的存在, 叶片两边是相通的. Chen等[16-17]研究了单个叶片在一个圆柱形容器里的构型并发现在接触角给定的情况下, 缝隙也存在一个临界值.只有当缝隙小于或等于其临界值时，平衡自由面不存在，从而保证叶片式管理装置的功能.
Concus-Finn方法有助于了解单值有限高度的平衡自由面在柱形容器里的存在性.如果要得到一个平衡曲面的具体形状, 或者如果容器的形状是三维的, 很多情况下需要借助于数值方法求解.在这方面, Surface Evolver[18-19]是一个很有效的数值工具.
2. 毛细力驱动的沿内角的流动分析
从上面的分析了解到在实际应用中, 当一个有限高度的单角柱形容器里部分充满液体, 液体满足γ < π/2-α并在指向容器底部的重力约束下达到平衡状态, 当重力突然消失时, 液体会沿着内角向容器顶部自发地流动.这种自发性的流动是受毛细力的驱动而不需要另外的装置(比如说液体泵), 从而在微重力液体推进剂管理装置和其他液体管理系统的设计里得到广泛应用.
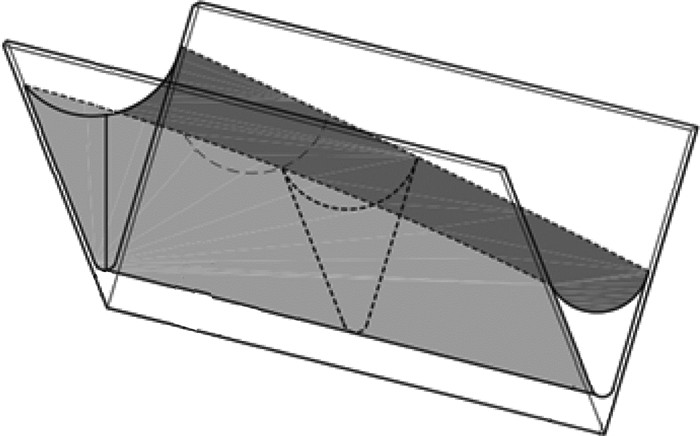
毛细力驱动的沿内角的流动(以下简称为内角流)也广泛存在于微尺度下, 典型的例子如在开放的V型沟槽[20]和与石油开采联系紧密的多孔介质内的流动[21].由于这些原因, 内角流一直是毛细流动现象研究中的焦点之一.需要指出的是, 本文探讨的是在黏性力和毛细力作用下充分发展的内角流.如图 9所示, 由于液体沿着内角的细长体形状, 流动可以被合理地假设为和壁面上固体液体和气体相交的接触线平行, 从而避免了建立动态接触线模型的困难, 结果是可以利用润滑理论直接模拟和流动方向垂直的液体横截面上的二维流动.早期数值模拟的主要目标是获取黏性力导致的流阻的定量了解.由于计算得到的流阻对于相关的几何参数如接触角和内角的角度非常敏感[22-23], 使得对流动的进一步分析变得很困难. Romero等[24]以及Weislogel等[25]利用尺度分析和摄动法[26-27]在理论分析上先后取得突破.
![]()
图 9 沿有钝度内角的毛细流动示意Figure 9. Schematic view of capillary flowalong a sharp interior corner图 9所示的内角有一定的钝度, 先分析钝度为0的情况.上面描述的内角流(又称毛细上升流)的一个独特之处是液面在内角对称面上一个固定位置的沿x轴方向的高度是一个常数H.这个固定位置叫做恒高点, 如图 10所示.从恒高点到液面端点的沿z轴的距离L尽管未知, 但是提供了一个长度尺度.二者的比值定义为ε=H/L.具体地说, 流动在3个坐标轴方向的长度尺度为x~H, y~Htanα, z~L, 如图 11所示.根据Young方程, 假设ε2f«1, 压力的尺度可以取为σ/(fH), 其中f是α和γ的函数, fH是在恒高点处代表液面的圆弧的半径.流动速度未知, 所以速度尺度不是事先给定的, 但为了进一步的流动分析它又是必要的.惯性力在流动开始的短期内不可忽略, 这里流动的长期特性是由黏性力和毛细力主控的.假设速度尺度为W, 如果忽略惯性力而只考虑黏性力, 沿着流动z方向的N-S方程的尺度化形式可以写成
![]()
图 10 沿内角的毛细上升流落塔实验图片,液体沿着容器右边的内角流动, 在恒高点液面离z轴的距离为常数Figure 10. Drop tower experiment images showing capillaryrise flow along an interior corner, for the flow in the righthand side corner there is a constant height location on the free surface where the distance between the surface and z-axis remains constant during the flow![]()
图 11 无钝度内角流动横截面上的长度尺度示意Figure 11. Schematic view of length scales on cross section of the flow along sharp interior corner\frac{\sigma }{{fHL}} \sim \left( {\frac{W}{{{H^2}}} + \frac{W}{{{H^2}{{\tan }^2}\alpha }}} \right) (7) 从中可以得到一个速度尺度W~εσsin2α/μ f.除了流体特性参数σ和μ, W还涵括了几何参数H, L, α, γ.
利用上述的尺度对N-S方程进行无量纲化, z方向的方程变为
A\frac{{{\rm{D}}{\mathcal{w}^*}}}{{{\rm{D}}{t^*}}} = - \frac{{{\rm{d}}{p^*}}}{{{\rm{d}}{z^*}}} + {\nabla ^2}{\mathcal{w}^*} (8) 系数A=Suε2sin4α/f, 其中Su=σρH/μ2是Suratman数.采用润滑理论并利用摄动法, 假设A和ε2同阶, 并且ε2«1，那么N-S方程的0阶方程为z方向的
\frac{{{\rm{d}}{p^*}}}{{{\rm{d}}{z^*}}} = \mathcal{w}_{oxx}^*{\sin ^2}\alpha + \mathcal{w}_{oyy}^*{\cos ^2}\alpha (9) 以及相应的边界条件包括在液体自由面上的剪切和法向应力边界条件[25].在0阶上, 自由面在x*-y*平面上的形状可以假设为一圆弧, 相应地, 法向压强po*以及圆弧自由面So*可以表达为
p_o^* = - \frac{1}{{{h^*}}} (10) S_o^* = {h^*}(1 + f) - f{h^*}{\left[{1-{{\left( {\frac{{{y^*}\tan \alpha }}{{f{h^*}}}} \right)}^2}} \right]^{\frac{1}{2}}} (11) f = {\left( {\frac{{\cos \gamma }}{{\sin \alpha }} - 1} \right)^{ - 1}} (12) 注意自由面在内角对称面上的高度h*还是一个未知变量.为了最终求解速度wo*和h*, 需要用沿z*方向的质量守恒方程
\frac{{\partial w_o^*}}{{\partial {t^*}}} = - \frac{{\partial \dot Q_o^*}}{{\partial {z^*}}} = - \frac{\partial }{{\partial {z^*}}}A_o^* < {\overline wo}{ > ^*} (13) 和方程Ao=h2.结合方程(9) 和(10), 液体在x*-y*平面上的0阶平均速度<wo>*最终可以表达为
< {w_o}{ > ^*} = - {F_i}{h^*}^2\frac{{\partial p_o^*}}{{\partial {z^*}}} = - {F_i}\frac{{\partial {h^*}}}{{\partial {z^*}}} (14) 这里的黏性阻尼系数Fi > 0是α和γ的函数.可以通过求解方程(9) 而得到Fi.对于α接近于0或π/2这两种情形可以用摄动法求得Fi的渐进解, 对于其他的α值, 可以用数值方法求解或者通过对文献中的数据进行转化而得到[25].尺度分析的最终目标是使得无量纲变量和1同阶, 换言之就方程(14) 而言，< wo > *~O(1),\partialh*/\partialz*~O(1), Fi~O(1).可以展示在满足Concus-Finn条件的前提下,1/8 ≤ Fi> ≤ 1/6,或者说Fi可以被视为一个和1同阶的常数.相应地方程(13)变为
2\frac{{\partial {h^*}}}{{\partial t}} = {F_i}\left[{2{{\left( {\frac{{\partial {h^*}}}{{\partial {z^*}}}} \right)}^2} + {h^*}\frac{{{\partial ^2}{h^*}}}{{\partial {z^{*2}}}}} \right] (15) 如果把系数Fi通过τ=Fit/2代入得到
\frac{{\partial {h^*}}}{{\partial \tau }} = 2{\left( {\frac{{\partial {h^*}}}{{\partial {z^*}}}} \right)^2} + {h^*}\frac{{{\partial ^2}{h^*}}}{{\partial {z^{*2}}}} (16) 此方程被称为液体自由面的进化方程, 由于描述的是扩散现象, 它和描述非定常热传导的主控方程的形式类似.方程(16) 在定常流动(h=h(z))的情况下可以直接求解, 除此之外在不同的边界条件下还有相似解.对于本文讨论的内角上升流可以通过相似变换
{h^*} = F(\eta ),\eta = {z^*}{(2\tau )^{ - 1/2}},{L_{_{{\text{tip}}}}} = {\eta _{{\text{tip}}}}{(2\tau )^{1/2}} (17) 把方程(16)转化为
F{F_{\eta \eta }} + 2F_\eta ^2 + \eta {F_\eta } = 0 (18) 以及边界条件
F(0) = 1, F({\eta _{{\rm{tip}}}}) = 0 (19) 其中, ηtip为自由面端点的位置, 由于它是一个未知量, 可以用一个体积积分约束
{F_\eta }{|_{\eta = 0}} = - \frac{1}{2}\int {_0^{{\eta _{{\rm{tip}}}}}{F^2}{\rm{d}}} \eta (20) 来闭合方程(18), 其解以及自由面端点相似解位置ηtip=1.702可以通过数值方法得到.方程(17) 的第3个关系式给出随时间变化的自由面端点位置\mathcal{L} tip, 转化为有量纲形式可以写为
\mathcal{L} = 1.702{G^{\frac{1}{2}}}{H^{\frac{1}{2}}}{t^{\frac{1}{2}}} (21) 同时也可以得到流量的表达式
\dot Q = 0.349{F_A}{G^{\frac{1}{2}}}{H^{\frac{5}{2}}}{t^{ - \frac{1}{2}}} (22) 其中,
\begin{array}{l} G = \frac{{\sigma {F_i}{{\sin }^2}\alpha }}{{\mu f}}, {F_A} = {f^2}(\frac{{\cos \gamma \sin \delta }}{{\sin \alpha }} - \delta )\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta = \pi /2 - \alpha - \gamma \end{array} (23) 关于其他的毛细流动现象的解具体参看文献[25].
至此可以看出通过有效的尺度分析最终得到关于流动的解析关系式诸如方程(21) 和(22).这些关系式一方面定量地把握住了相关参数对流动的影响, 加深了对这类流动现象的理解; 另一方面为相关流动系统的设计提供了简洁有力的定量分析手段与优化工具.
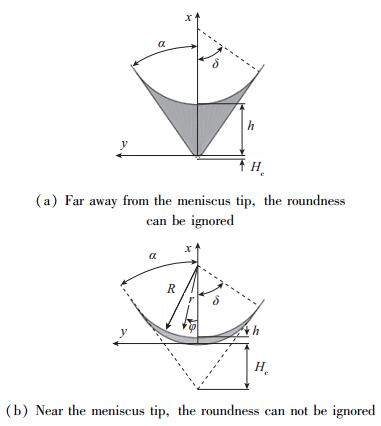
在上面的分析里, 每一个相关变量的尺度都既是全局性的也是局部性的, 或者说尺度是单一的.比如说x和y的尺度不论是在远离还是靠近自由面端点的部位都适用, 因为流动横截面的形状在两个部位具有相似性.这种单一尺度在沿着带有钝度的内角的毛细流里失效. Chen等[28]发现单一尺度的选择不能保证Fi变化很小并且和1同阶, 从而为进一步的流动分析带来困难.如图 12所示, 在远离自由面端点的部位, Hc/(h+Hc)1, 流动的横截面上内角的圆度可以被忽略, 接近于没有钝度的内角并且流动在横截面上的变化是二维的.但是在靠近端点的部位, Hc/(h+Hc)→1, 内角钝度的影响变得异常突出, 以至于流动横截面的形状发生质的变化, 接近于一层弯月形薄膜并且流动在横截面上的变化几乎是一维的.流动横截面在这两种情况下不再具有相似性.这个显著变化使得单一尺度不再普遍适用.为了解决这个问题引入当地尺度和全局尺度的概念.
![]()
图 12 有钝度内角流动横截面的两种极限状况Figure 12. Two limited cases of cross section of flow along a rounded interior corner当地尺度指的是用当地的已知或未知的相关参数或变量作为尺度.例如, 根据观察, 如图 13所示, x和y方向的当地尺度可以取为
![]()
图 13 钝内角流动横截面上的当地长度尺度Figure 13. Local length scales on cross section of flow along a rounded interior cornerx \sim h (24) y \sim h\tan \alpha + {H_c}{f_c}\delta (25) 这里Rc=Hcfc代表内角钝度的圆弧的半径, 液面高度h是未知变量并且是z的函数.有了这两个关键尺度, 其他相关变量的当地尺度可以一一求得.类似于上面的对无钝度内角流动的分析步骤, 主控方程可以用当地尺度进行无量纲化，从而给出当地的流动方程.最关心的依然是流动横截面上当地无量纲的平均速度
< \overline w { > ^*} = \frac{1}{{\overline {{A^*}} }}\iint{\overline w ^*}{\rm{d}}{\overline x ^*}{\rm{d}}{\overline y ^*} (26) 这里变量名上方的横线用来代表当地的量, 星号代表无量纲的量.类似地, 该平均速度的一般解可以用数值方法求得, 渐近解则可以用摄动法求得.在接触角γ=0时, 对于h,Hc和α的所有可能值, 可以显示0.117≤<\overline w>*≤0.229，从而可以被当作和1同阶的常数处理.
下一步, 需要把当地的无量纲平均速度转换成全局的无量纲平均速度.这一步是必要的, 因为当地的尺度是未知的并且随z变化, 而全局的尺度是已知的.在x和y方向的全局尺度可以选为
x \sim H \sim {H_c} (27) y \sim \left( {H \sim {H_c}} \right)\tan \alpha + Hcf\delta (28) 相应地, 可以得到当地和全局的无量纲平均速度之间的转换关系式
< w{ > ^*} = - {F_i}\frac{{\partial {h^*}}}{{\partial {z^*}}} (29) {F_i} = \frac{{ < \overline w { > ^*}}}{{k_\lambda ^2}}{\left( {\frac{{1 + {k_\delta }\overline \lambda }}{{1 + \overline \lambda }}} \right)^2}\;\;\frac{{1 + k_\lambda ^2{T^2}}}{{1 + {{(1 + k\delta \overline \lambda )}^2}{{\tan }^2}\alpha }} (30) 其中,
\overline \lambda = \frac{\lambda }{{\left( {1 - \lambda } \right){h^*}}}, T = \frac{{\tan \alpha }}{{1 - \lambda }} (31) {k_\delta } = \frac{{f\delta }}{{\tan \alpha }}, {k_\lambda } = 1 - \lambda + {k_{_\delta }}\lambda (32) 在前面分析没有钝度的内角流动已经发现Fi可以被当作一个常数处理, 但是由于 \overline w*可以被当作常数处理, 方程(30) 给出Fi>在有钝度的内角流动里的解析表达式.相应地类似于方程(16) 却复杂很多的自由面的进化方程可以求得[28].方程(16) 在内角的钝度很小或者 \overline\lambda是一个高阶小量时是沿有钝度的内角的毛细流的自由面进化方程的一个极限情形.对于本文讨论的内角上升流动后者依然有相似解[28], 并且解析解和落塔实验结果比较接近[29].
由于运用了当地和全局尺度, 方程(30) 捕捉到了流动阻尼函数Fi和相关变量之间的关系，从而使进一步的流动解析解成为可能.当地和全局尺度方法的实质是为横截面上流动的黏性力项里的Laplace算子提供了一个尺度从而可以求得一个有效的速度尺度.这个方法因此被称作Laplace算子尺度方法[30].在许多情况下, Laplace算子尺度方法优于经典的水力直径方法.
液体在内角由于毛细力的作用而产生自发流动, 使内角在微尺度或微重力的流动系统中有广泛应用.上述的分析内角流动的方法和结果不仅可以应用到横截面均一的有内角的容器或管道, 包括叶片式推进剂管理装置, 也可以应用到液体在内角的毛细扩张[31]毛细复合流动[32]和毛细流, 比如气泡在横截面相似按比例逐渐变化的有内角的弱三维容器或管道里的迁移[33].
3. 结论
内角作为一个简单有效的基本几何元素为自发性的毛细流动提供通道而得到广泛应用, 一个典型的例子是航天飞行器液体燃料箱内部的推进剂管理装置.与毛细现象相关的静力学方面的发展，尤其是对无限高柱形容器内的平均曲率处处相等单值有限高度的平衡毛细曲面的存在性的研究，为实际应用与设计提供了有效的定量分析工具.尺度方法为沿内角的毛细流动的动力学特性的理论分析带来新的进展.本文回顾的方法适用于在细长容器或管道内沿着内角的毛细流, 流动可以假设为平行, 从而动态接触角的效应可以被忽略.相应的流动解析解为数值计算提供基准并为设计提供快捷的参考和有效的优化工具.新的挑战来自于当容器或管道呈强三维或内部形状的复杂性增加以及在非零度接触角状况下的接触角滞后等非线性效应.这些挑战对发展有效的数值分析工具提出新的要求.
致谢: 感谢倪招勇研究员审阅并鼓励完成此文，感谢Andrew Wollman博士帮助绘制图 3. -
![]()
图 1 液体燃料箱内的叶片式推进剂管理装置示意
Figure 1. Schematic view of vane type propellant management device inside a fuel tank
![]()
图 2 液体燃料箱叶片式推进剂管理装置横截面
Figure 2. Cross-sectional view of vane type propellant management device
![]()
图 3 横截面均一的柱形容器内的毛细面示意
(没有显示毛细面下方的液体)
Figure 3. Schematic view of capillary surface within a cylindrical container of uniform cross section
(liquid below capillary surface is not shown)
![]()
图 4 流体压强和交界面弯曲方向的关系
Figure 4. Sketches showing the relation between pressure difference and direction in which a surface curves
![]()
图 5 二维单角柱形容器的横截面形状
Figure 5. Cross section of a two-dimensional cylindrical container with a single corner
![]()
图 6 二维单角柱形容器的横截面和液面的交界线
Figure 6. Intersection line between cross section of a two-dimensional cylindrical container with a single corner and a liquid surface
![]()
图 7 计算得到的单角柱形容器里的液体和气体之间的
Figure 7. Numerical results of capillary surface shape in container with single corner (the liquid below the capillary surface is not shown)
![]()
图 8 二维单角柱形容器横截面
Figure 8. Cross section domain of a two-dimensional cylindrical container with single corner
![]()
图 9 沿有钝度内角的毛细流动示意
Figure 9. Schematic view of capillary flowalong a sharp interior corner
![]()
图 10 沿内角的毛细上升流落塔实验图片,液体沿着容器右边的内角流动, 在恒高点液面离z轴的距离为常数
Figure 10. Drop tower experiment images showing capillaryrise flow along an interior corner, for the flow in the righthand side corner there is a constant height location on the free surface where the distance between the surface and z-axis remains constant during the flow
![]()
图 11 无钝度内角流动横截面上的长度尺度示意
Figure 11. Schematic view of length scales on cross section of the flow along sharp interior corner
![]()
图 12 有钝度内角流动横截面的两种极限状况
Figure 12. Two limited cases of cross section of flow along a rounded interior corner
-
[1] de Gennes P G, Brochard-Wyart F, Quere D. Capillarity and wetting phenomena: drops, bubbles, pearls, waves[M]. New York: Springer-Verlag, 2004.
[2] Finn R. Capillary surface interfaces[J]. Notices of the American Mathematical Society, 1999, 46(7): 770-781.
[3] Myshkis A D, Babskii V G, Kopachevskii N D, et al. Low-gravity fluid mechanics[M]. Berlin: Springer-Verlag, 1986.
[4] Jaekle Jr D E. Propellant management device conceptual design and analysis: vanes[R]. AIAA 1991-2172, 1991.
[5] Jaekle Jr D E. Propellant management device conceptual design and analysis: sponges[R]. AIAA 1993-1970, 1993.
[6] Jaekle Jr D E. Propellant management device conceptual design and analysis: traps and troughs[C]. 31st AIAA Joint Propulsion Conference and Exhibit, San Diego: 1995.
[7] Jaekle Jr D E. Propellant management device conceptual design and analysis: galleries[R]. AIAA 1997-2811, 1997.
[8] Concus P, Finn R. On capillary free surfaces in a gravitational field[J]. Acta Mathematica, 1974, 132(1): 207-223. https://www.researchgate.net/publication/225436662_On_capillary_free_surfaces_in_a_gravitational_field
[9] Concus P, Finn R.On capillary free surfaces in the absence of gravity[J]. Acta Mathematica, 1974, 132(1): 177-198. https://www.researchgate.net/publication/226869670_On_capillary_free_surfaces_in_the_absence_of_gravity
[10] Concus P, Finn R. On the behavior of a capillary surface in a wedge[J]. Proceedings of the National Academy of Sciences, 1969, 63(2): 292-299. DOI: 10.1073/pnas.63.2.292
[11] Finn R. Equilibrium capillary surfaces[M]. New York: Springer-Verlag, 1986.
[12] Finn R, Weston Neel R. C-singular solutions of the capillary problem[J]. Journal Fur Die Reine Und Angewandte Mathematik, 1999, 512: 1-26. https://www.researchgate.net/publication/2676031_Singular_Solutions_of_the_Capillary_Problem
[13] de Lazzer A, Langbein D, Dreyer M, et al. Mean curvature of liquid surfaces in cylindrical containers of arbitrary cross-section[J]. Microgravity Science and Technology, 1996, 9(3): 208-219. https://www.researchgate.net/publication/37916033_Mean_Curvature_of_Liquid_Surfaces_in_Cylindrical_Containers_of_Arbitrary_Cross-Section
[14] Concus P, Finn R. Dichotomous behavior of capillary surfaces in zero gravity[J]. Microgravity Science and Technology, 1990, 3(2): 87-92.
[15] Concus P, Finn R. Capillary surfaces in a wedge-differing contact angles[J]. Microgravity Science and Technology, 1993, 7(2): 152-155.
[16] Chen Y, Collicott S H. Investigation of the symmetric wetting of vane-wall gaps in propellant tanks[J]. AIAA Journal, 2004, 42(2): 305-314. DOI: 10.2514/1.915
[17] Chen Y, Collicott S H. Study of wetting in an asymmetrical vane-wall gap in propellant tanks[J]. AIAA Journal, 2006, 44(4): 859-867. DOI: 10.2514/1.15729
[18] Brakke K A. The surface evolver[J]. Experimental Mathematics, 1992, 1(2): 141-165. DOI: 10.1080/10586458.1992.10504253
[19] Chen Y, Schaeffer B M, Weislogel M M, et al. Introducing SE-FIT: surface evolver-fluid interface tool for studying capillary surfaces[R]. AIAA 2011-1319, 2011.
[20] Mann J A, Romero L, Rye R R, et al. Flow of simple liquids down narrow V grooves[J]. Physical Review E, 1995, 52(4): 3967-3972. DOI: 10.1103/PhysRevE.52.3967
[21] AI-Futaisi A, Patzek T W. Three-phase hydraulic conductances in angular capillaries[C]. SPE/DOE Improved Oil Recovery Symposium, Tulsa, 2002.
[22] Dong M, Chatzis I. The imbibition and flow of a wetting liquid along the corners of a square capillary tube[J]. Journal of Colloid and Interface Science, 1995, 172: 278-288. DOI: 10.1006/jcis.1995.1253
[23] Ayyaswamy P S, Catton I, Edwards D K. Capillary flow in triangular grooves[J]. Transactions of the ASME Journal of Applied Mechanics, 1974, 41: 332-336. DOI: 10.1115/1.3423288
[24] Romero L A, Yost G G. Flow in an open channel capillary[J]. Journal of Fluid Mechanics, 1996, 322: 109-129. DOI: 10.1017/S0022112096002728
[25] Weislogel M M, Lichter S. Capillary flow in an interior corner[J]. Journal of Fluid Mechanics, 1998, 373: 349-378. DOI: 10.1017/S0022112098002535
[26] Bejan A. Convection heat transfer[M]. 3rd edition. New York: Wiley, 2004.
[27] Lin C C, Segel L A. Mathematics applied to deterministic problems in the natural sciences[M]. Society for Industrial and Applied Mathematics, 1988.
[28] Chen Y, Weislogel M M, Nardin C L. Capillary-driven flows along rounded interior corners[J]. Journal of Fluid Mechanics, 2006, 566: 235-271. DOI: 10.1017/S0022112006001996
[29] Chen Y, Weislogel M M, Bolleddula D A. Capillary flow in cylindrical containers with rounded interior corners[R]. AIAA 2007-0745, 2007.
[30] Weislogel M M, Chen Y, Bolleddula D. A better non-dimensionalization scheme for slender laminar flows: the Laplacian operator scaling method[J]. Physics of Fluids, 2008, 20(9): 93602. DOI: 10.1063/1.2973900
[31] Weislogel M M, Lichter S. A spreading drop in an interior corner: theory and experiment[J]. Microgravity Science and Technology, 1996, 9(3): 175-184. https://www.researchgate.net/publication/285878393_A_spreading_drop_in_an_interior_corner_Theory_and_experiment
[32] Weislogel M M, Baker J A, Jenson R M. Quasi-steady capillarity-driven flows in slender containers with interior edges[J]. Journal of fluid mechanics, 2011, 685: 271-305. DOI: 10.1017/jfm.2011.314
[33] Weislogel M M, Compound capillary rise[J]. Journal of Fluid Mechanics, 2012, 709: 622-647. DOI: 10.1017/jfm.2012.357
-
期刊类型引用(1)
1. 杨恩博，金宇鹏，杨光，黄永华，王天祥，雷刚，吴静怡. 内角钝度对微重力下液体推进剂毛细流动特性的影响. 上海交通大学学报. 2023(06): 739-746 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 78
- HTML全文浏览量: 20
- PDF下载量: 5
- 被引次数: 1
邮件订阅
RSS