大膨胀比喷管性能工程估算方法

黄蓉; 贾要强; 李斌

doi:10.19527/j.cnki.2096-1642.1009

大膨胀比喷管性能工程估算方法

北京动力机械研究所, 北京 100074

详细信息

作者简介:
黄蓉(1992-) 女, 博士, 高工, 主要研究方向为高超声速流体力学、进排气设计。E-mail: hrong321@163.com

中图分类号: V41
计量
- 文章访问数: 140
- HTML全文浏览量: 44
- PDF下载量: 20
出版历程
- 收稿日期: 2022-09-05
- 修回日期: 2023-01-08

Engineering Estimation Method of Large Expansion Ratio Nozzle Performance

Beijing Power Machinery Institute, Beijing 100074, China

摘要

摘要: 针对大膨胀比尾喷管, 基于等熵假设、流量守恒, 结合分离预测公式, 发展了考虑分离的喷管性能工程估算方法, 并利用数值仿真对文章的性能评估方法进行了验证, 结果表明, 考虑分离方法估算的推力性能随落压比的变化趋势与数值模拟结果基本一致, 能够较好地评估大膨胀比喷管的性能上限, 有效地弥补了过膨胀程度较高的低落压比工况下的推力性能预测能力, 同时提高了高落压比范围的预测精度, 可以为喷管设计提供直接指导。
- 大膨胀比 /
- 尾喷管 /
- 分离 /
- 性能估算 /
- 数值仿真
Abstract: Based on isentropic assumption, mass conservation and separation prediction formula, an engineering estimation method of nozzle performance considering flow separation was developed for large expansion ratio nozzle, and the performance evaluation method was verified with numerical simulation in this paper. The variation trend of thrust performance with nozzle pressure ratio(NPR) estimated by present method is in good agreement with simulation results. The results indicate that the present method has a good predicting ability at highly over-expanded flow conditions and an accurate estimation on large NPR state. It can provide direct guidance for nozzle design.
- large expansion ratio /
- nozzle /
- separation /
- performance estimation /
- numerical simulation

HTML全文

0. 引言

超燃冲压、火箭等飞行器高空飞行时，尾喷管入口总压与环境压力的比值(落压比)可达500以上，为了获得足够的高空推力性能，尾喷管往往采用大膨胀比设计，使得流动尽可能等熵地膨胀到环境压力。

在高空设计点附近，大膨胀比尾喷管处于大落压比欠膨胀状态，推力性能可以利用等熵膨胀理论进行一维等熵评估。李俊红等^[1]基于这种理想估算开展了对发动机推力预测工程方法的研究，常璐等^[2]基于数值模拟的数据建立了矢量喷管的性能预测模型，徐惊雷、王占学等分别研究了飞行Mach数、入口Mach数构型等多种因素影响下的推力性能^[3-8]。然而，如图 1所示，当大膨胀比尾喷管几何不可调时，在爬升或下降过程中，由于过大的面积扩张比与较小的工作落压比不匹配，大膨胀比尾喷管处于过膨胀状态，流动发生大分离^[9-12]，膨胀效率随工作落压比会发生很大变化。此时，利用一维等熵膨胀理论估算的结果将大大偏离实际情况，不利于发动机设计初期的性能评估。目前，针对大膨胀比尾喷管的推力性能，尚未有研究给出考虑大分离的性能评估方法。

图 1 喷管不同落压比下的压力云图

Figure 1. Contours of nozzle pressure under different NPR

下载: 全尺寸图片幻灯片

为了更准确地评估大膨胀比喷管在不同落压比下的工作特性，本文结合过膨胀分离预测方法，围绕最大推力设计的轴对称大膨胀比喷管，发展了考虑流动分离的固定几何大膨胀比喷管性能工程估算方法。

1. 喷管模型

首先利用Rao最大推力设计方法^[13-14]，设计了轴对称喷管，作为性能评估对象。如图 2所示，出口截面与喉道截面面积膨胀比AR为10，扩张段长度L与喉道半径R_th之比为6.3，设计落压比为96.5。

图 2 大膨胀比喷管模型

Figure 2. Schematics of large expansion ratio nozzle

下载: 全尺寸图片幻灯片

2. 喷管性能评估方法

本节首先从推力系数定义出发，结合流量公式和等熵关系式，推导一维等熵评估方法，获得一维等熵推力系数评估曲线；继而结合分离预测准则与等熵关系，确定过膨胀状态分离点的参数；然后针对本文设计的最大推力大膨胀比喷管模型，提取壁面参数分布规律，基于分离点上游压力积分，建立考虑分离的推力性能评估方法，最后获得大膨胀比喷管的推力系数曲线。

2.1 一维等熵推力性能评估

一般地，截面富裕冲量I为

$I=\dot{m} v+A\left(P-P_{\mathrm{a}}\right)$

其中， $\dot{m}$ 为截面质量流量，v为截面速度，A为截面面积，P为截面静压，P_a为环境压力。理想推力I_ideal定义为喷管等熵膨胀到环境压力时的富裕冲量，故其表达式为

$I_{\text {ideal }}=\dot{m} v_{\text {ideal }}$

其中，下标ideal表示理想出口截面。利用总压P_t和喉道面积A_th对理想推力I_ideal进行无量纲。对于量热完全气体来说，根据流量公式和等熵关系式，可以推导无量纲理想推力表达式为

$\frac{I_{\text {ideal }}}{A_{\text {th }} P_{\mathrm{t}}}=K^{\prime} \sqrt{\left(1-\left(\frac{P_{\mathrm{t}}}{P_{\mathrm{a}}}\right)^{-\frac{\gamma-1}{\gamma}}\right) \frac{2}{\gamma-1}}$

其中，γ为气体比热比，K′为

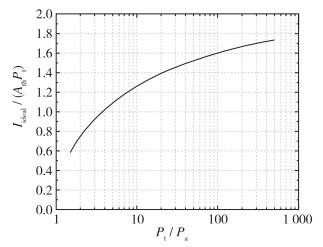
$K^{\prime}=\gamma \sqrt{\left(\frac{2}{\gamma+1}\right)^{\frac{\gamma+1}{\gamma-1}}}$

从无量纲理想推力表达式中可以看出其大小与比热比γ和落压比NPR=P_t/P_a有关，如图 3所示，随着落压比增大，无量纲理想推力逐渐增大。

图 3 无量纲理想推力曲线

Figure 3. Profile of dimensionless ideal trust

下载: 全尺寸图片幻灯片

针对设计喷管面积膨胀比为AR_d的大膨胀比喷管，一般地，将其等熵膨胀至出口截面时的无量纲推力I_e/(A_thP_t)与无量纲理想推力的比值定义推力系数C_Ix，来衡量喷管推力性能或者膨胀效率。对于量热完全气体来说，推力系数计算方法为

$\begin{array}{r} \mathrm{AR}=\frac{A_{\mathrm{e}}}{A_{\mathrm{th}}}=\frac{1}{q\left(M a_{\mathrm{e}}\right)} \\ \frac{I_{\mathrm{e}}}{A_{\mathrm{th}} P_{\mathrm{t}}}=\frac{\dot{m} v_{\mathrm{e}}+A_{\mathrm{e}}\left(P_{\mathrm{e}}-P_{\mathrm{a}}\right)}{A_{\mathrm{th}} P_{\mathrm{t}}}= \end{array}$

$\begin{gathered} K^{\prime} M a_{\mathrm{e}} \sqrt{\frac{1}{1+\frac{\gamma-1}{2} M a_{\mathrm{e}}^2}}+\frac{1}{q\left(M a_{\mathrm{e}}\right)}\left(\frac{P_{\mathrm{e}}}{P_{\mathrm{t}}}-\frac{P_{\mathrm{a}}}{P_{\mathrm{t}}}\right) \\ C_{I x}=\left(\frac{I_{\mathrm{e}}}{A_{\mathrm{th}} P_{\mathrm{t}}}\right) /\left(\frac{I_{\text {ideal }}}{A_{\mathrm{th}} P_{\mathrm{t}}}\right) \end{gathered}$

其中，下标e表示出口截面参数，q(Ma_e)为流量函数。

利用上述公式，给出基于等熵膨胀假设的推力系数。如图 4所示，在给定AR_d下，推力系数在小落压比时随着落压比的上升，推力系数先上升，后下降，在设计落压比NPR_d时最大；AR_d越大，设计落压比NPR_d越大，小落压比时推力系数越低，大落压比时推力系数越高。可以看出，若不考虑流动分离，仅基于等熵膨胀假设评估的大膨胀比喷管，在小落压比工作时，其推力系数很低，甚至可以为负值。

图 4 一维等熵推力系数曲线

Figure 4. Profile of 1D isentropic thrust coefficient

下载: 全尺寸图片幻灯片

2.2 分离点的确定

考虑喷管的分离流动时，Schmucker分离准则^[15]被广泛应用于预测喷管分离，其表达式为

$\frac{P_{\text {sep }}}{P_{\mathrm{a}}}=\left(1.88 M a_{\text {sep }}-1\right)^{-0.64}$

其中，下标sep表示分离点当地参数。该式描述了喷管分离点上游附近的Mach数和当地压力与背压之比的关系。

另一方面，根据等熵关系式，喷管分离点上游任意位置的Mach数和压力与背压之比满足如下关系

$\frac{P_{\text {sep }}}{P_{\mathrm{a}}}=\frac{P_{\text {sep }}}{P_{\mathrm{t}}} \cdot \frac{P_{\mathrm{t}}}{P_{\mathrm{a}}}=\left(1+\frac{\gamma-1}{2} M a_{\text {sep }}^2\right)^{-\frac{\gamma}{\gamma-1}} \cdot \frac{P_{\mathrm{t}}}{P_{\mathrm{a}}}$

利用上述两式，可以求得任意落压比下分离点上游附近的Ma_sep，图 5给出AR_d=10的分离Mach数随落压比的变化曲线，落压比低于设计落压比时，流动为过膨胀状态，Ma_sep随落压比逐渐增大；落压比高于设计落压比时，流动不分离，将Ma_sep设置为设计出口Mach数，约为3.49。

图 5 AR_d=10分离Mach数与落压比的关系曲线

Figure 5. Relation between separation Mach number and NPR (AR_d=10)

下载: 全尺寸图片幻灯片

2.3 考虑分离推力性能评估

当流动发生分离时，喷管分离点后的压力可近似认为与环境压力相等，从而忽略分离点下游的型面产生推力，喷管推力由分离点之前的喷管扩张壁面产生，可通过壁面压力积分得到，则喷管分离时的无量纲推力为

$\begin{aligned} & \frac{I_{\text {sep }}}{A_{\mathrm{th}} P_{\mathrm{t}}}=\frac{I_{\mathrm{th}}+F_x}{A_{\mathrm{th}} P_{\mathrm{t}}} \\ & =\frac{I_{\mathrm{th}}+\int_{A_{\mathrm{th}}}^{A_{\text {sep }}}\left(P_{\text {sep }}-P_{\mathrm{a}}\right) \mathrm{d} A}{A_{\mathrm{th}} P_{\mathrm{t}}} \\ & =K^{\prime} \sqrt{\frac{\gamma}{1+\frac{\gamma-1}{2}}}+\left(1+\frac{\gamma-1}{2}\right)^{-\frac{\gamma}{\gamma-1}}+ \\ & \int\limits_1^{A_{\text {sep }} / A_{\mathrm{th}}}\left(1+\frac{\gamma-1}{2} M a_{\text {sep }}^2\right)^{-\frac{\gamma}{\gamma-1}} \mathrm{~d} A-\frac{A_{\text {sep }}}{A_{\mathrm{th}}} \frac{P_{\mathrm{a}}}{P_{\mathrm{t}}} \\ & \end{aligned}$

其中，A为壁面任意位置处从喉道到扩张段壁面在轴线方向的投影面积，F_x为喷管壁面受到的轴线推力，沿流向为正。可以看出，喷管分离时的无量纲推力仅与分离点上游的当地Mach数随截面积的分布、落压比两个参数有关。

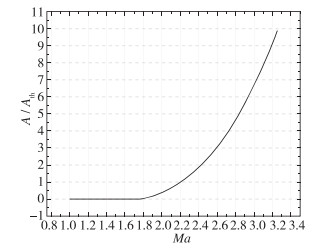
在利用特征线方法设计大膨胀比喷管模型时，可以得到沿程的喷管扩张段壁面轴向投影面积与当地Mach数的关系，如图 6所示。通过3次公式拟合，得到关系式为

图 6 轴向投影面积与当地Mach数关系

Figure 6. Relation between axial projected area and local Mach number

下载: 全尺寸图片幻灯片

$\frac{A}{A_{\mathrm{th}}}=\left\{\begin{array}{cc} 0 & M a \leqslant 1.62 \\ 1.154 M a^3-4.01 M a^2+4.357 M a-1.442 & 1.62<M a \leqslant 3.25 \end{array}\right.$

3次拟合公式相关系数R²=0.999。

综上，当落压比小于设计落压比时，结合分离喷管无量纲推力公式和大膨胀比Rao喷管轴向投影面积与当地Mach数关系，即可估算考虑分离的推力系数；当落压比大于设计落压比时，流动不分离，仍然采用一维等熵推力系数进行估算。

2.4 大膨胀比喷管推力系数

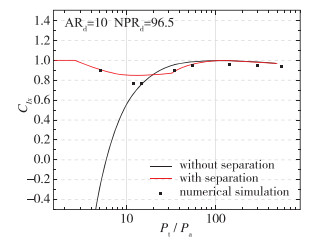
针对本文的性能评估对象，即设计膨胀比10、设计落压比96.5的大膨胀比喷管，利用本文方法，估算出其推力系数曲线。如图 7所示，在落压比小于6时，不考虑分离的预测结果出现负值，不符合实际情况，故该方法此时失效；当落压比小于20时，考虑分离的预测结果均在0.8以上，远高于不考虑分离的推力系数；在落压比超过20时，考虑分离的推力系数低于不考虑分离的推力系数；随着工作压比增大，分离Mach数逐渐接近设计出口Mach数，推力系数逐渐接近不考虑分离的推力系数。

图 7 大膨胀比喷管推力系数曲线

Figure 7. Profile of large expansion ratio nozzle thrust coefficient

下载: 全尺寸图片幻灯片

3. 方法验证

针对本文的大膨胀比喷管，利用二维轴对称数值模拟开展不同落压比下喷管性能的计算。计算时，湍流模型选用k-ω SST模型，通量格式采用Roe格式，空间离散格式采用2阶迎风格式，第1层网格高度0.05 mm时，网格总数量约为1.0×10⁵。图 8给出数值模拟的典型落压比下的Mach数云图，随着落压比升高，流动的分离逐渐消失。

图 8 典型落压比Mach数云图

Figure 8. Mach number contours under typical NPR

下载: 全尺寸图片幻灯片

统计数值模拟计算结果得到推力系数，与大膨胀比喷管推力系数曲线对比，如表 1和图 9所示。数值模拟得到的推力系数分布趋势与考虑分离的分布趋势基本一致：本文的大膨胀比喷管推力系数在过膨胀程度较高的低落压比工况(NPR=5)时，推力系数约为0.922；随着落压比增大逐渐下降，到NPR=11左右达到最低值，约为0.767；保持一段较低水平后逐渐回升，在设计点附近达到最高；最后随着欠膨胀程度加剧而缓慢下降。

表 1 推力系数预测方法与数值模拟结果对比

Table 1. Comparison of thrust coefficient between engineering estimation and numerical simulation

NPR	CFD	with separation	error	without separation	error
5.0	0.899	0.907	0.9%	—	—
11.8	0.767	0.850	10.88%	0.660	-13.91%
14.7	0.774	0.847	9.46%	0.764	-1.25%
34.4	0.903	0.889	-1.59%	0.958	6.04%
54.2	0.949	0.958	0.94%	0.989	4.21%
141.3	0.964	0.998	3.46%	0.998	3.40%
299.5	0.952	0.983	3.24%	0.983	3.11%

下载: 导出CSV

| 显示表格

图 9 数值模拟与工程估算方法对比

Figure 9. Comparison between numerical simulation and engineering estimation

下载: 全尺寸图片幻灯片

对比一维等熵预测方法与数值模拟结果，可以看出，过膨胀程度较高的低落压比工况(NPR=5)时，不考虑分离的预测方法失效，而考虑分离的预测方法误差仅为-1.61%；中等落压比(NPR=11.8, 14.7)时，考虑分离的预测结果偏高，误差大小在10%左右，不考虑分离的预测结果随落压比变化较大，与数值模拟结果趋势上差异较大，计算工况中误差最高可达13.91%；高落压比(NPR=34.4, 54.2)时，考虑分离的预测误差在2%以内，预测精度明显高于不考虑分离预测方法的6.04%，误差降低至接近原来的1/4；在欠膨胀阶段(NPR=141.3, 299.5)，两者基本一致，误差不超过4%。这表明一维等熵估算和考虑分离工程估算方式的结合，一方面给出了低落压比工况下的推力性能预测方法，另一方面提高了大膨胀比喷管的推力性能预测精度。

4. 结论

本文针对大膨胀比尾喷管，基于等熵假设、流量守恒，结合分离预测公式，发展了考虑分离的喷管性能工程估算方法，估算了大膨胀比尾喷管的推力性能，最后利用数值仿真对本文的性能评估方法进行了验证，结果表明：

1) 考虑分离方法估算的推力性能随落压比变化趋势与数值模拟结果基本一致，均在低落压比工况时推力系数较高，随着落压比增大逐渐下降，到中等落压比时达到最低而后逐渐回升，在设计点附近达到最高，最后随着欠膨胀程度加剧而缓慢下降；

2) 与不考虑分离的一维等熵估算方法相比，本文方法有效地弥补了过膨胀程度较高的低落压比工况下的推力性能预测能力，同时提高了高落压比范围的预测精度，高落压比(NPR=34.4, 54.2)时，误差约为不考虑分离估算方法的1/4，可为喷管设计提供直接指导。

图 1 喷管不同落压比下的压力云图

Figure 1. Contours of nozzle pressure under different NPR

下载: 全尺寸图片幻灯片

图 2 大膨胀比喷管模型

Figure 2. Schematics of large expansion ratio nozzle

下载: 全尺寸图片幻灯片

图 3 无量纲理想推力曲线

Figure 3. Profile of dimensionless ideal trust

下载: 全尺寸图片幻灯片

图 4 一维等熵推力系数曲线

Figure 4. Profile of 1D isentropic thrust coefficient

下载: 全尺寸图片幻灯片

图 5 AR_d=10分离Mach数与落压比的关系曲线

Figure 5. Relation between separation Mach number and NPR (AR_d=10)

下载: 全尺寸图片幻灯片

图 6 轴向投影面积与当地Mach数关系

Figure 6. Relation between axial projected area and local Mach number

下载: 全尺寸图片幻灯片

图 7 大膨胀比喷管推力系数曲线

Figure 7. Profile of large expansion ratio nozzle thrust coefficient

下载: 全尺寸图片幻灯片

图 8 典型落压比Mach数云图

Figure 8. Mach number contours under typical NPR

下载: 全尺寸图片幻灯片

图 9 数值模拟与工程估算方法对比

Figure 9. Comparison between numerical simulation and engineering estimation

下载: 全尺寸图片幻灯片

表 1 推力系数预测方法与数值模拟结果对比

Table 1 Comparison of thrust coefficient between engineering estimation and numerical simulation

NPR	CFD	with separation	error	without separation	error
5.0	0.899	0.907	0.9%	—	—
11.8	0.767	0.850	10.88%	0.660	-13.91%
14.7	0.774	0.847	9.46%	0.764	-1.25%
34.4	0.903	0.889	-1.59%	0.958	6.04%
54.2	0.949	0.958	0.94%	0.989	4.21%
141.3	0.964	0.998	3.46%	0.998	3.40%
299.5	0.952	0.983	3.24%	0.983	3.11%

下载: 导出CSV

参考文献(15)

[1]	李俊红, 程晓丽, 沈清. 超燃冲压发动机性能预测工程方法[J]. 推进技术, 2009, 30(2): 129-134, 164. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS200902001.htm Li J H, Cheng X L, Shen Q. Engineering method of scramjet engine performance prediction based on nozzle exit pressure[J]. Journal of Propulsion Technology, 2009, 30(2): 129-134, 164(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS200902001.htm
[2]	常璐, 额日其太, 杨亚雄. 基于数值模拟的轴对称矢量喷管性能预测数学模型[J]. 航空动力学报, 2017, 32(4): 909-916. https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI201704018.htm Chang L, Eriqitai, Yang Y X. Mathematical model of performance prediction of axisymmetric vectoring nozzle based on numerical simulations[J]. Journal of Aerospace Power, 2017, 32(4): 909-916(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI201704018.htm
[3]	张艳慧, 徐惊雷, 张堃元. 超燃冲压发动机非对称喷管设计点性能[J]. 推进技术, 2007, 28(3): 282-286. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS200703013.htm Zhang Y H, Xu J L, Zhang K Y. Numerical simulation of single expansion ramp nozzle for scramjet on the designing point[J]. Journal of Propulsion Technology, 2007, 28(3): 282-286(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJJS200703013.htm
[4]	徐惊雷, 张艳慧, 张堃元. 超燃冲压发动机非对称喷管非设计状态性能计算[J]. 推进技术, 2007, 28(3): 287-290. DOI: 10.3321/j.issn:1001-4055.2007.03.015 Xu J L, Zhang Y H, Zhang K Y. Numerical simulation of single expansion ramp nozzle for scramjet on the off-design point[J]. Journal of Propulsion Technology, 2007, 28(3): 287-290(in Chinese). DOI: 10.3321/j.issn:1001-4055.2007.03.015
[5]	汪维娜, 王占学, 乔渭阳. 单斜面膨胀喷管几何参数对流场和性能的影响[J]. 航空动力学报, 2006, 21(2): 280-284. DOI: 10.3969/j.issn.1000-8055.2006.02.009 Wang W N, Wang Z X, Qiao W Y. Investigation of the influence of single expansion ramp nozzle geometric parameters on the flow field and performance[J]. Journal of Aerospace Power, 2006, 21(2): 280-284(in Chinese). DOI: 10.3969/j.issn.1000-8055.2006.02.009
[6]	Perrier P, Rapuc M, Rostand P, et al. Nozzle and afterbody design for hypersonic airbreathing vehicles[R]. AIAA 96-4548, 1996.
[7]	李建平, 宋文艳, 陈亮. 超燃冲压发动机尾喷管性能研究[J]. 机械设计与制造, 2008(2): 95-97. https://www.cnki.com.cn/Article/CJFDTOTAL-JSYZ200802041.htm Li J P, Song W Y, Chen L. Research on characteristic of nozzle in scramjet[J]. Machinery Design & Manufacture, 2008(2): 95-97(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JSYZ200802041.htm
[8]	文科, 李旭昌, 马岑睿, 等. 不同入口马赫数对超燃冲压发动机尾喷管的性能影响研究[J]. 火箭推进, 2011, 37(3): 18-21. https://www.cnki.com.cn/Article/CJFDTOTAL-HJTJ201103003.htm Wen K, Li X C, Ma C R, et al. Influence of nozzle inlet Mach number on performance of scramjet nozzle[J]. Journal of Rocket Propulsion, 2011, 37(3): 18-21(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HJTJ201103003.htm
[9]	Frey M, Hagemann G. Restricted shock separation in rocket nozzles[J]. Journal of Propulsion and Power, 2000, 16(3): 478-484.
[10]	Hagemann G, Frey M, Koschel W. Appearance of restricted shock separation in rocket nozzles[J]. Journal of Propulsion and Power, 2002, 18(3): 577-584.
[11]	李耿, 侯晓, 陈慧, 等. 固体火箭发动机喷管分离流场数值模拟及试验研究[J]. 固体火箭技术, 2013, 36(3): 324-328. https://www.cnki.com.cn/Article/CJFDTOTAL-GTHJ201303008.htm Li G, Hou X, Chen H, et al. Analysis of numerical si-mulation and test of the separated flow field in solid rocket motor nozzle[J]. Journal of Solid Rocket Techno-logy, 2013, 36(3): 324-328(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GTHJ201303008.htm
[12]	黄宏艳, 王强. 过膨胀状态下轴对称收-扩喷管内外流场计算及分析[J]. 航空动力学报, 2007, 22(7): 1069-1073. https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200707008.htm Huang H Y, Wang Q. Numerical investigation on internal and external flows for axisymmetric convergent-divergent nozzles on over-expansion state[J]. Journal of Aerospace Power, 2007, 22(7): 1069-1073(in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200707008.htm
[13]	Rao G V R. Exhaust nozzle contour for optimum thrust[J]. Journal of Jet Propulsion, 1958, 28(6): 377-382.
[14]	Rao G V R, Beck J E, Booth T E. Nozzle optimization for space-based vehicles[R]. AIAA 99-2584, 1999.
[15]	Schmucker R H. Status of flow separation prediction in liquid propellant rocket nozzles[R]. NASA TM X-64890, 1974.

施引文献(2)

期刊类型引用(2)

1.	张耐民，许昊，孙铁志，孔德才，李芳. 不同共流条件下过膨胀水下超声速气体喷流试验研究. 导弹与航天运载技术(中英文). 2025(01): 8-16 . 百度学术
2.	高惊涛，孙宏权，李新艳，王宁飞. 入口流场不均匀性对固体火箭发动机大膨胀比喷管内流场的影响. 固体火箭技术. 2024(04): 547-556 . 百度学术

其他类型引用(0)

资源附件(0)

图(9) / 表(1)

计量

文章访问数: 140
HTML全文浏览量: 44
PDF下载量: 20
被引次数: 2

0. 引言
1. 喷管模型
2. 喷管性能评估方法
2.1 一维等熵推力性能评估
2.2 分离点的确定
2.3 考虑分离推力性能评估
2.4 大膨胀比喷管推力系数
3. 方法验证
4. 结论

主管部门：	中国航天科技集团有限公司
主办单位：	中国航天空气动力技术研究院中国宇航学会中国宇航出版有限责任公司

大膨胀比喷管性能工程估算方法

作者简介:
黄蓉(1992-) 女, 博士, 高工, 主要研究方向为高超声速流体力学、进排气设计。E-mail: hrong321@163.com

计量